Exam 13: Functions of Several Variables
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Find 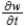 using the appropriate Chain Rule for
using the appropriate Chain Rule for 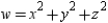 where
where 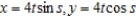 , and
, and 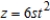 .
.
Free
(Multiple Choice)
4.8/5  (35)
(35)
Correct Answer:
A
Use Lagrange multipliers to find the minimum distance from the plane 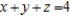 to the point
to the point 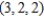 . Round your answer to two decimal places.
. Round your answer to two decimal places.
Free
(Multiple Choice)
4.8/5  (32)
(32)
Correct Answer:
D
Find a unit normal vector to the surface 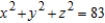 at the point
at the point 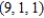 .
.
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
D
Find the second partial derivative for the function 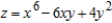 with respect to x.
with respect to x.
(Multiple Choice)
4.8/5  (39)
(39)
Use Lagrange multipliers to minimize the function 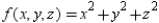 subject to the following two constraints.
subject to the following two constraints. 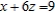
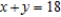 Assume that x, y, and z are nonnegative.
Assume that x, y, and z are nonnegative.
(Multiple Choice)
4.8/5  (36)
(36)
Find symmetric equations of the normal line to the surface 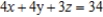 at the point
at the point 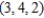 .
.
(Multiple Choice)
4.9/5  (35)
(35)
Examine the function 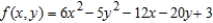 for relative extrema and saddle points.
for relative extrema and saddle points.
(Multiple Choice)
4.8/5  (28)
(28)
Use Lagrange multipliers to find the maximum value of 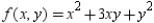 where
where 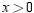 and
and 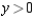 subject to the constraint
subject to the constraint 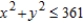 .
.
(Multiple Choice)
4.9/5  (28)
(28)
Find the critical points of the function 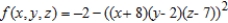 , and from the form of the function, determine whether a relative maximum or a relative minimum occurs at each point.
, and from the form of the function, determine whether a relative maximum or a relative minimum occurs at each point.
(Multiple Choice)
4.8/5  (28)
(28)
For 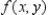 , find all values of x and y such that
, find all values of x and y such that 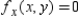 and
and 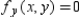 simultaneously.
simultaneously. 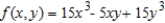
(Multiple Choice)
4.9/5  (29)
(29)
Find the maximum value of the directional derivative at the point 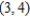 of the function
of the function 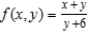 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (27)
(27)
Use Lagrange multipliers to find the minimum distance from the parabola 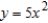 to the point
to the point 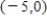 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.9/5  (29)
(29)
Find the minimum cost of producing 60,000 units of a product 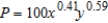 , where x is the number of units of labor (at $80 per unit) and y is the number of units of capital (at $40 per unit). Round your answer to the nearest cent.
, where x is the number of units of labor (at $80 per unit) and y is the number of units of capital (at $40 per unit). Round your answer to the nearest cent.
(Multiple Choice)
4.9/5  (32)
(32)
Use Lagrange multipliers to find the maximum value of 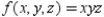 where
where 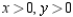 and
and 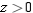 , subject to the constraint
, subject to the constraint 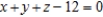 .
.
(Multiple Choice)
4.9/5  (39)
(39)
Suppose a corporation manufactures candles at two locations. The cost of producing 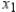 units at location 1 is
units at location 1 is 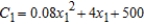 and the cost of producing
and the cost of producing 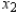 units at location 2 is
units at location 2 is 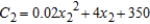 . The candles sell for $12 per unit. Find the quantity that should be produced at each location to maximize the profit
. The candles sell for $12 per unit. Find the quantity that should be produced at each location to maximize the profit 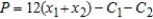 .
.
(Multiple Choice)
4.7/5  (46)
(46)
The radius of a right circular cylinder is increasing at a rate of 8 inches per minute, and the height is decreasing at a rate of 6 inches per minute. What is the rate of change of the surface area when the radius is 16 inches and the height is 37 inches?
(Multiple Choice)
5.0/5  (37)
(37)
Showing 1 - 20 of 173
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)