Exam 14: Multiple Integration
Exam 1: Preparation for Calculus125 Questions
Exam 2: Limits and Their Properties85 Questions
Exam 3: Differentiation193 Questions
Exam 4: Applications of Differentiation154 Questions
Exam 5: Integration184 Questions
Exam 6: Differential Equations93 Questions
Exam 7: Applications of Integration119 Questions
Exam 8: Integration Techniques and Improper Integrals130 Questions
Exam 9: Infinite Series181 Questions
Exam 10: Conics, Parametric Equations, and Polar Coordinates114 Questions
Exam 11: Vectors and the Geometry of Space130 Questions
Exam 12: Vector-Valued Functions85 Questions
Exam 13: Functions of Several Variables173 Questions
Exam 14: Multiple Integration143 Questions
Exam 15: Vector Anal142 Questions
Select questions type
Write a double integral that represents the surface area of 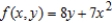 over the region R: triangle with vertices
over the region R: triangle with vertices 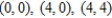 . Use a computer algebra system to evaluate the double integral. Round your answer to two decimal places.
. Use a computer algebra system to evaluate the double integral. Round your answer to two decimal places.
Free
(Multiple Choice)
4.9/5  (37)
(37)
Correct Answer:
B
Evaluate the iterated integral 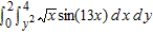 by switching the order of integration. Round your to three decimal places.
by switching the order of integration. Round your to three decimal places.
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
A
Find the mass of the lamina described by the inequalities 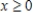 and
and 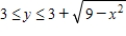 , given that its density is
, given that its density is 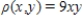 .
(Hint: Some of the integrals are simpler in polar coordinates.)
.
(Hint: Some of the integrals are simpler in polar coordinates.)
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
A
Use a triple integral to find the volume of the solid bounded by the graphs of the equations 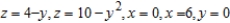 .
.
(Multiple Choice)
4.9/5  (36)
(36)
Set up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations 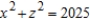 and
and 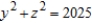 in the first octant.
in the first octant.
(Multiple Choice)
4.7/5  (36)
(36)
Find the mass of the triangular lamina with vertices 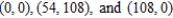 for the density
for the density 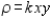 .
.
(Multiple Choice)
4.9/5  (34)
(34)
Find the center of mass of the lamina bounded by the graphs of the equations 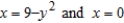 for the density
for the density 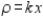 .
.
(Multiple Choice)
4.8/5  (28)
(28)
Use a change of variables to find the volume of the solid region lying below the surface 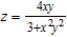 and above the plane region R: region bounded by the graphs of
and above the plane region R: region bounded by the graphs of 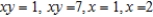 (Hint: Let
(Hint: Let 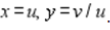 .) Round your answer to two decimal places.
.) Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Use cylindrical coordinates to find the volume of the solid inside both 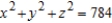 and
and 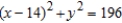 .
.
(Multiple Choice)
4.7/5  (38)
(38)
Use a double integral in polar coordinates to find the volume of the solid inside the hemisphere 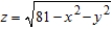 but outside the cylinder
but outside the cylinder 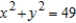 .
.
(Multiple Choice)
4.8/5  (31)
(31)
Set up a triple integral that gives the moment of inertia about the 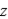 -axis of the solid region Q of density given below.
-axis of the solid region Q of density given below. 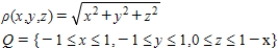
(Multiple Choice)
4.7/5  (37)
(37)
Use a change of variables to find the volume of the solid region lying below the surface 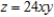 and above the plane region R: region bounded by the square with vertices
and above the plane region R: region bounded by the square with vertices 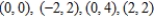 .
.
(Multiple Choice)
4.8/5  (28)
(28)
Set up and evaluate a double integral to find the volume of the solid bounded by the graphs of the equations given below. 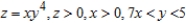
(Multiple Choice)
4.8/5  (40)
(40)
Use a change of variables to find the volume of the solid region lying below the surface 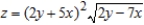 and above the plane region R: region bounded by the parallelogram with vertices
and above the plane region R: region bounded by the parallelogram with vertices 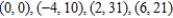 . Round your answer to two decimal places.
. Round your answer to two decimal places.
(Multiple Choice)
4.8/5  (32)
(32)
Set up an integral for both orders of integration, and use the more convenient order to evaluate the integral below over the region R. 
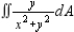

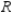
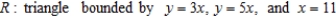
(Multiple Choice)
4.9/5  (38)
(38)
Use a double integral to find the volume of the indicated solid. 
(Multiple Choice)
4.8/5  (32)
(32)
Use an iterated integral to find the area of the region shown in the figure below. 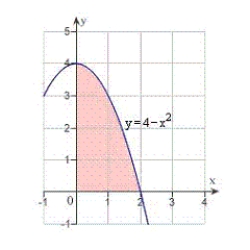
(Multiple Choice)
4.9/5  (44)
(44)
Showing 1 - 20 of 143
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)