Exam 6: Applications of Definite Integrals
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
B
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the y-axis.
-
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
A
Find the volume of the solid generated by revolving the region about the y-axis.
-The region in the first quadrant bounded on the left by , on the right by the line , and above by the line
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
C
Find the volume of the solid generated by revolving the region about the given line.
-The region in the first quadrant bounded above by the line , below by the curve , and on the left by the -axis, about the line
(Multiple Choice)
4.9/5  (34)
(34)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by
(Multiple Choice)
4.9/5  (36)
(36)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the x-axis.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume that remains after a hole of radius 1 is bored through the center of a solid sphere of radius
(Multiple Choice)
4.9/5  (33)
(33)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region in the first quadrant bounded on the left by , on the right by the line , and below by the -axis
(Multiple Choice)
4.7/5  (40)
(40)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by the triangle with vertices
(Multiple Choice)
4.8/5  (42)
(42)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the -axis at and . The cross sections perpendicular to the -axis between these planes are squares whose bases run from the parabola to the parabola
(Multiple Choice)
4.9/5  (39)
(39)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the -axis at and . The cross sections perpendicular to the -axis are circular disks whose diameters run from the parabola to the parabola .
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid generated by revolving the region about the given line.
-The region in the first quadrant bounded above by the line , below by the curve , and on the left by the -axis, about the line
(Multiple Choice)
4.8/5  (35)
(35)
Find the volume of the described solid.
-The base of a solid is the region between the curve and the -axis from to . The cross sections perpendicular to the -axis are squares with bases running from the -axis to the curve.
(Multiple Choice)
4.8/5  (40)
(40)
The hemispherical bowl of radius 5 contains water to a depth 4 . Find the volume of water in the bowl.
(Multiple Choice)
4.7/5  (34)
(34)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the x-axis.
-
(Multiple Choice)
4.8/5  (37)
(37)
Find the volume of the solid generated by revolving the region about the given line.
-The region bounded above by the line , below by the curve , and on the right by the line , about the line
(Multiple Choice)
4.9/5  (36)
(36)
Find the volume that remains after a hole of radius 1 is bored through the center of a solid cylinder of radius 2 and height 4 .
(Multiple Choice)
4.8/5  (44)
(44)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the x-axis.
-
(Multiple Choice)
4.9/5  (46)
(46)
Find the volume of the solid generated by revolving the region about the given line.
-The region bounded above by the line , below by the curve , on the left by the line , and on the right by the line , about the line
(Multiple Choice)
4.8/5  (30)
(30)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated line.
-About the line
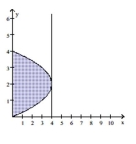
(Multiple Choice)
4.8/5  (39)
(39)
Showing 1 - 20 of 115
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)