Exam 6: Applications of Definite Integrals
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the x-axis.
- , for
(Multiple Choice)
4.9/5  (43)
(43)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by
(Multiple Choice)
5.0/5  (40)
(40)
A water tank is formed by revolving the curve about the -axis. Find the volume of water in the tank as a function of the water depth, .
(Multiple Choice)
4.9/5  (43)
(43)
Find the volume of the described solid.
-The solid lies between planes perpendicular to the -axis at to . The cross sections perpendicular to the -axis are circular disks with diameters running from the curve to the curve .
(Multiple Choice)
4.9/5  (35)
(35)
An auxiliary fuel tank for a helicopter is shaped like the surface generated by revolving the curve , , about the -axis (dimensions are in feet). If a cubic foot holds gallons and the helicopter gets 3 miles to the gallon, how many additional miles will the helicopter be able to fly once the tank is installed (to the nearest mile)?
(Multiple Choice)
4.9/5  (30)
(30)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the x-axis.
-
(Multiple Choice)
4.9/5  (44)
(44)
Find the volume of the solid generated by revolving the region about the y-axis.
-The region enclosed by
(Multiple Choice)
4.9/5  (39)
(39)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the -axis
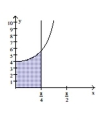
(Multiple Choice)
4.7/5  (43)
(43)
Find the volume of the described solid.
-The base of a solid is the region between the curve and the -axis from to . The cross sections perpendicular to the -axis are squares with diagonals running from the -axis to the curve.
(Multiple Choice)
4.7/5  (37)
(37)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
4.8/5  (38)
(38)
A water tank is formed by revolving the curve about the -axis. Water drains from the tank through a small hole in the bottom of the tank. At what constant rate does the water level, , fall? (Use Torricelli's Law: .)
(Multiple Choice)
4.9/5  (43)
(43)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
5.0/5  (37)
(37)
Find the volume of the solid generated by revolving the region about the given line.
-The region in the second quadrant bounded above by the curve , below by the -axis, and on the right by the -axis, about the line
(Multiple Choice)
4.7/5  (41)
(41)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the y-axis.
-
(Multiple Choice)
4.8/5  (47)
(47)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.
-About the -axis
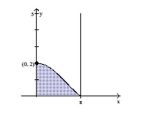
(Multiple Choice)
4.9/5  (36)
(36)
Find the volume of the described solid.
-The base of the solid is the disk . The cross sections by planes perpendicular to the -axis between and are isosceles right triangles with one leg in the disk.
(Multiple Choice)
4.7/5  (35)
(35)
Use the shell method to find the volume of the solid generated by revolving the shaded region about the indicated axis.
-About the -axis
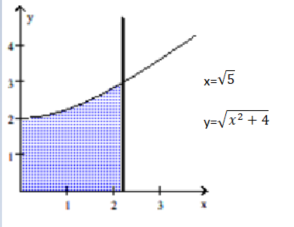
(Multiple Choice)
4.8/5  (36)
(36)
Find the volume of the solid generated by revolving the shaded region about the given axis.
-About the -axis
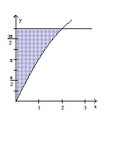
(Multiple Choice)
4.8/5  (33)
(33)
Find the volume of the solid generated by revolving the region bounded by the given lines and curves about the x-axis.
-
(Multiple Choice)
4.9/5  (33)
(33)
Use the shell method to find the volume of the solid generated by revolving the region bounded by the given curves and
lines about the y-axis.
-
(Multiple Choice)
4.9/5  (43)
(43)
Showing 41 - 60 of 115
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)