Exam 4: Applications of Derivatives
Exam 1: Functions124 Questions
Exam 2: Limits and Derivatives213 Questions
Exam 3: Differentiation183 Questions
Exam 4: Applications of Derivatives159 Questions
Exam 5: Integration107 Questions
Exam 6: Applications of Definite Integrals115 Questions
Exam 7: Integrals and Transcendental Functions114 Questions
Exam 8: Techniques of Integration124 Questions
Exam 9: First-Order Differential Equations75 Questions
Exam 10: Infinite Sequences and Series155 Questions
Select questions type
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
- Round to the nearest thousandth.
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
D
Determine all critical points for the function.
-
Free
(Multiple Choice)
4.9/5  (38)
(38)
Correct Answer:
B
Use the following function and a graphing calculator to answer the questions.
![Use the following function and a graphing calculator to answer the questions. f ( x ) = \sqrt { 2 x } + 1.1 \sin x , [ 0,2 \pi ] \text { a). Plot the function over the interval to see its general behavior there. Sketch the graph below. } b). Find the interior points where f' = 0 (you may need to use the numerical equation solver to approximate a solution). You may wish to plot f' as well. List the points as ordered pairs (x, y). c). Find the interior points where f' does not exist. List the points as ordered pairs (x, y). d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y). e). Find the function's absolute extreme values on the interval and identify where they occur.](https://storage.examlex.com/TB8583/11ece0bf_b59c_303e_8008_6d21c6205cbf_TB8583_11.jpg) b). Find the interior points where f' = 0 (you may need to use the numerical equation solver to approximate a
solution). You may wish to plot f' as well. List the points as ordered pairs (x, y).
c). Find the interior points where f' does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
b). Find the interior points where f' = 0 (you may need to use the numerical equation solver to approximate a
solution). You may wish to plot f' as well. List the points as ordered pairs (x, y).
c). Find the interior points where f' does not exist. List the points as ordered pairs (x, y).
d). Evaluate the function at the endpoints and list these points as ordered pairs (x, y).
e). Find the function's absolute extreme values on the interval and identify where they occur.
Free
(Essay)
4.8/5  (34)
(34)
Correct Answer:
a). 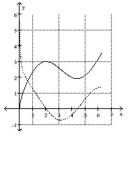
Solid line: ; dashed line:
b). See figure above. at and .
Critical points of are and .
c). is undefined at the endpoint .
d). Endpoints are and .
e). Absolute minimum: ; absolute maximum .
Determine from the graph whether the function has any absolute extreme values on the interval [a, b].
-![Determine from the graph whether the function has any absolute extreme values on the interval [a, b]. -](https://storage.examlex.com/TB8583/11eb8c85_25d9_787c_8371_a1e5bc1b5ef0_TB8583_00.jpg)
(Multiple Choice)
4.8/5  (36)
(36)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
5.0/5  (29)
(29)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.8/5  (28)
(28)
Solve the problem.
-Find the graph that matches the given table.
x (x) -1.5 0 2 7
(Multiple Choice)
4.9/5  (27)
(27)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.8/5  (33)
(33)
Find the extreme values of the function and where they occur.
-
(Multiple Choice)
4.9/5  (33)
(33)
Sketch the graph of the function and determine whether it has any absolute extreme values on its domain.
-
(Multiple Choice)
4.8/5  (44)
(44)
Determine from the graph whether the function has any absolute extreme values on the interval [a, b].
-![Determine from the graph whether the function has any absolute extreme values on the interval [a, b]. -](https://storage.examlex.com/TB8583/11eb8c85_25d9_516a_8371_6522c9eb316c_TB8583_00.jpg)
(Multiple Choice)
4.9/5  (28)
(28)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.8/5  (38)
(38)
Solve the problem.
-Find the table that matches the graph below.
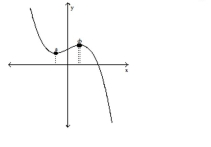
(Multiple Choice)
4.7/5  (33)
(33)
Find the value or values of that satisfy the equation in the conclusion of the Mean Value Theorem for the function and interval.
-If the derivative of an even function f(x) is zero at x = c, can anything be said about the value of f' at x = -c? Givereasons for your answer.
(Essay)
4.9/5  (28)
(28)
Find the absolute extreme values of the function on the interval.
-
(Multiple Choice)
4.9/5  (27)
(27)
Identify the function's local and absolute extreme values, if any, saying where they occur.
-
(Multiple Choice)
4.9/5  (36)
(36)
Find the derivative at each critical point and determine the local extreme values.
-
(Multiple Choice)
4.9/5  (29)
(29)
Use the maximum/minimum finder on a graphing calculator to determine the approximate location of all local extrema.
-
(Multiple Choice)
4.9/5  (32)
(32)
Find the absolute extreme values of the function on the interval.
-f(x) = 3x - 4, -2 x 3
(Multiple Choice)
4.9/5  (35)
(35)
Showing 1 - 20 of 159
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)