Exam 5: Analytic Trigonometry
Exam 1: Functions and Their Graphs119 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions40 Questions
Exam 4: Trigonometric Functions40 Questions
Exam 5: Analytic Trigonometry40 Questions
Exam 6: Additional Topics in Trigonometry40 Questions
Exam 7: Linear Systems and Matrices40 Questions
Exam 8: Sequences, Series, and Probability40 Questions
Exam 9: Topics in Analytic Geometry40 Questions
Exam 10: Analytic Geometry in Three Dimensions40 Questions
Exam 11: Calculus Practice Problems120 Questions
Select questions type
Find the exact solutions of the given equation in the interval .
Free
(Multiple Choice)
4.8/5  (27)
(27)
Correct Answer:
D
Find the exact value of given that and . (Both and are in Quadrant II.)
Free
(Multiple Choice)
4.7/5  (46)
(46)
Correct Answer:
C
If , use trigonometric substitution to write as a trigonometric function of , where .
Free
(Multiple Choice)
5.0/5  (29)
(29)
Correct Answer:
B
Determine which of the following are trigonometric identities.
I.
II.
III.
(Multiple Choice)
4.9/5  (41)
(41)
Find the exact value of given that and . (Both and are in Quadrant II.)
(Multiple Choice)
4.9/5  (35)
(35)
Determine which of the following are trigonometric identities.
I.
II.
III.
(Multiple Choice)
4.9/5  (36)
(36)
Add or subtract as indicated; then use fundamental identities to simplify the expression below and determine which of the following is not equivalent.
(Multiple Choice)
4.9/5  (37)
(37)
Use the trigonometric substitution to write the expression as a trigonometric function of , where .
(Multiple Choice)
4.7/5  (33)
(33)
Find the exact solutions of the given equation in the interval .
(Multiple Choice)
4.9/5  (35)
(35)
Use the figure below to determine the exact value of the given function.
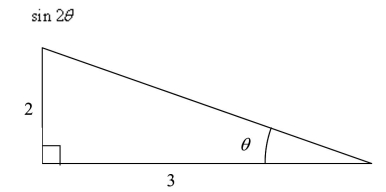
(Multiple Choice)
4.9/5  (36)
(36)
Showing 1 - 20 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)