Exam 5: Analytic Trigonometry
Exam 1: Functions and Their Graphs119 Questions
Exam 2: Polynomial and Rational Functions120 Questions
Exam 3: Exponential and Logarithmic Functions40 Questions
Exam 4: Trigonometric Functions40 Questions
Exam 5: Analytic Trigonometry40 Questions
Exam 6: Additional Topics in Trigonometry40 Questions
Exam 7: Linear Systems and Matrices40 Questions
Exam 8: Sequences, Series, and Probability40 Questions
Exam 9: Topics in Analytic Geometry40 Questions
Exam 10: Analytic Geometry in Three Dimensions40 Questions
Exam 11: Calculus Practice Problems120 Questions
Select questions type
Use the product-to-sum formula to write the given product as a sum or difference.
(Multiple Choice)
4.8/5  (38)
(38)
Which of the following is a solution to the given equation?
(Multiple Choice)
4.8/5  (36)
(36)
Find the exact value of given that and . (Both and are in Quadrant IV.)
(Multiple Choice)
4.8/5  (32)
(32)
Use a double angle formula to rewrite the following expression.
(Multiple Choice)
4.9/5  (35)
(35)
Find the exact value of given that and . (Both and are in Quadrant IV.)
(Multiple Choice)
4.8/5  (34)
(34)
Approximate the solutions of the equation by considering its graph below. Round your answer to one decimal.
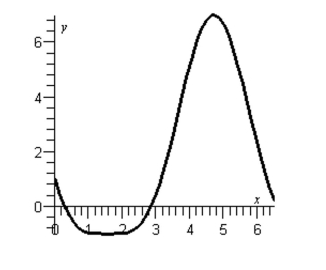
(Multiple Choice)
4.8/5  (35)
(35)
Use the figure below to find the exact value of the given trigonometric expression.
(Multiple Choice)
4.8/5  (34)
(34)
Expand the expression below and use fundamental trigonometric identities to simplify.
(Multiple Choice)
4.8/5  (41)
(41)
Use the graph of the function to approximate the maximum points of the graph in the interval . Round your answer to one decimal.
![Use the graph of the function f ( x ) = - 2 \cos ( x ) + \sin ( x ) to approximate the maximum points of the graph in the interval [ 0,2 \pi ] . Round your answer to one decimal.](https://storage.examlex.com/TB8857/11ecd5cc_3846_c774_be5f_d58edf2c6f32_TB8857_11.jpg)
(Multiple Choice)
4.9/5  (34)
(34)
Use the half-angle formulas to determine the exact value of the following.
(Multiple Choice)
4.9/5  (39)
(39)
Determine which of the following are trigonometric identities. I.
II.
III.
IV.
(Multiple Choice)
4.7/5  (42)
(42)
Factor; then use fundamental identities to simplify the expression below and determine which of the following is not equivalent.
(Multiple Choice)
4.8/5  (48)
(48)
Find all solutions of the following equation in the interval .
(Multiple Choice)
4.8/5  (47)
(47)
Which of the following is a solution to the given equation?
(Multiple Choice)
4.9/5  (39)
(39)
Use a double-angle formula to find the exact value of when , where .
(Multiple Choice)
4.9/5  (33)
(33)
Showing 21 - 40 of 40
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)