Exam 8: Testing the Difference Between Two Means, Two Proportions, and Two Variances

$\sqrt { \frac { \sigma _ { 1 } } { n _ { 1 } } + \frac { \sigma _ { 2 } } { n _ { 2 } } }$ The standard error of difference of two large (independent) sample means is

When the subjects are paired or matched in some way, samples are considered to be __________. ________________________________________

A study on the oxygen consumption rate (OCR) of sea cucumbers involved a random sample of size 10 at 15oC and second random sample of size 7 kept at 18oC. If one tested the hypothesis that this range of Temperature had no effect on the OCR (assume equal variability) the critical value would be (assume $a$ $=$ .05)

The campus bookstore asked a random set of freshmen and seniors how much they spent on textbooks for that term. The bookstore believes that the two groups spend the same amount. What is the test value? Freshmen Seniors Sample size 80 60 Mean spending 40 -15 Sample variance 400 800

Many elementary school students in a school district currently have ear infections. A random sample of children in two different schools found that 13 of 46 at one school and 15 of 30 at the other had this Infection. At the .05 level of significance, is there sufficient evidence to conclude that a difference exists Between the proportion of students who have ear infections at one school and the other?

$\text { Determine the value of } \alpha \text { as shown in the figure below, if the degrees of freedom were } 7 \text { and }$ 9.

One poll found that 41% of male voters will support a candidate while another found that 49% of female voters will be in support. To test whether this candidate has equal levels of support between male and Female voters, the null hypothesis should be

When subjects are matched according to one variable, the matching process does not eliminate the influence of other variables.

A researcher wanted to determine if using an octane booster would increase gasoline mileage. A random sample of seven cars was selected; the cars were driven for two weeks without the booster and two weeks with the booster. Miles / Gal Without Miles / Gal With 21.2 23.8 25.4 25.6 20.9 22.4 27.6 28.3 22.8 24.5 27.3 28.8 23.4 25.2 -A dietician investigated whether apples turned brown at different rates when exposed to air after being washed in hot water or in cold water. She took 12 random apples and cut each in half. She washed one Half of each apple in hot water and the other half in cold water, and then put both halves out in a tray. Her Results (in hours until turning a particular shade of brown) are in the table below. At 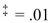, did she see a Difference between the two treatments? Hot Water Cold Water Difference by Apple Sample mean 6.00 5.95 -0.05 Sample variance 2.10 2.50 0.65

Compute the critical value for a right-tailed F -test with $a = 0.05 , \text { d.f.N. } = 21 , \text { and d.f.D. } = 20$

A pooled estimate of the variance is a weighted average of the variance using the two sample variances and the __________ of each variance as the weights. ________________________________________

The mean value of F is approximately equal to __________. ________________________________________

What is the null hypothesis? Use $\alpha = 0.05$ . Refer To: 09-18

70% of students at a university live on campus. A random sample found that 35 of 50 male students and 42 of 50 of female students lived on campus. At the .05 level of significance, is there sufficient evidence To conclude that a difference exists between the proportion of male students who live on campus and the Proportion of female students who live on campus?

A reporter bought a hamburger at each of a set of random stores of two different restaurant chains. She then had the number of calories in each hamburger measured. Can the reporter conclude, at $\ddagger=.05,$ that the two sets of hamburgers have different amounts of calories? (Use the equal variances formula.) Women Men Sample size 7 8 Mean spending amount 80 95 Sample variance 400 800

For the samples summarized below, test the hypothesis at $\ddagger=.05$ that the two variances are equal. Variance Number of data values Sample 1 29 9 Sample 2 10 19

A pharmaceutical company is testing the effectiveness of a new drug for lowering cholesterol. As part of this trial, they wish to determine whether there is a difference in effectiveness between women and men. Women Men Sample size 60 60 Mean effect 7.5 6.65 Sample variance 2.5 4

One poll found that 40% of male voters will support a candidate while another found that 48% of female voters will be in support. To test whether this candidate has equal levels of support between male and Female voters, the alternative hypothesis should be