Exam 6: Topics in Analytic Geometry
Exam 1: Functions and Their Graphs121 Questions
Exam 2: Polynomial and Rational Functions129 Questions
Exam 3: Exponential and Logarithmic Functions46 Questions
Exam 4: Trigonometry61 Questions
Exam 5: Analytic Trigonometry67 Questions
Exam 6: Topics in Analytic Geometry100 Questions
Select questions type
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
(Multiple Choice)
4.9/5  (28)
(28)
Select the curve represented by the parametric equations. (indicate the orientation of the curve) x=4-5t y=5+4t
(Multiple Choice)
4.7/5  (27)
(27)
Select the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.7/5  (40)
(40)
Find the standard form of the equation of the ellipse with the given characteristics and center at the origin. 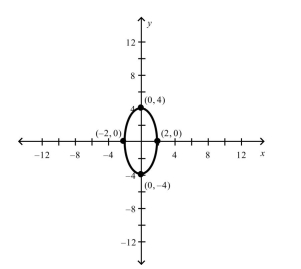
(Multiple Choice)
4.8/5  (36)
(36)
A point in polar coordinates is given. Convert the point to rectangular coordinates. Round your answers to one decimal places.
(Multiple Choice)
4.9/5  (36)
(36)
Consider a line with slope m and y-intercept Select the graph of the distance between the origin and the line.
(Multiple Choice)
4.9/5  (32)
(32)
By using a graphing utility select the correct graph of the polar equation. Identify the graph.
(Multiple Choice)
4.9/5  (32)
(32)
Select the graph of the polar equation using symmetry, zeros, maximum r-values, and any other additional points.
(Multiple Choice)
4.9/5  (31)
(31)
Use a graphing utility to find the rectangular coordinates of the point given in polar coordinates. Round your results to two decimal places.
(Multiple Choice)
4.9/5  (33)
(33)
Select the graph of the equation as a circle, a parabola, an ellipse, or a hyperbola.
(Multiple Choice)
4.8/5  (38)
(38)
A point in rectangular coordinates is given. Convert the point to polar coordinates.
(Multiple Choice)
4.8/5  (36)
(36)
Using following result find a set of parametric equation of the line.
Line: passes through and
(Multiple Choice)
4.7/5  (40)
(40)
Showing 81 - 100 of 100
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)