Exam 4: Systems of Equations and Inequalities
Exam 1: Basic Concepts306 Questions
Exam 2: Equations and Inequalities234 Questions
Exam 3: Graphs and Functions61 Questions
Exam 4: Systems of Equations and Inequalities116 Questions
Exam 5: Polynomials and Polynomial Functions112 Questions
Exam 6: Rational Expressions and Equations130 Questions
Exam 7: Roots, Radicals, and Complex Numbers298 Questions
Exam 8: Quadratic Functions221 Questions
Exam 9: Exponential and Logarithmic Functions229 Questions
Exam 10: Characteristics of Functions and Their Graphs142 Questions
Exam 11: Conic Sections132 Questions
Exam 12: Sequences, Series, and Probability208 Questions
Select questions type
Determine whether the ordered pair or ordered triple satisfies the system of linear equations.
- y=-3x-7 y=-x- (-4,-5)
(Multiple Choice)
4.9/5  (46)
(46)
Solve the problem.
-Jancie has $180,000 to invest to obtain annual income. She wants some of it invested in safe Certificates of Deposit yielding 7%. The rest she wants to invest in AA bonds yielding 11% per year. How much should she
Invest in each to realize exactly $17,400 per year?
(Multiple Choice)
5.0/5  (39)
(39)
Determine the solution to the system of inequalities.
- y<2x+2 y\leq-x
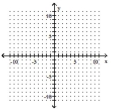
(Multiple Choice)
4.9/5  (38)
(38)
Solve the system of equations using the addition method.
- -0.2x+0.3y-0.3z=-2.8 0.4x-0.1y+0.2z=2 -0.2x-0.4y+0.4z=2.8
(Multiple Choice)
4.9/5  (35)
(35)
Solve the system of equations using the addition method.
- 5x+35y=35 9x-5y=-5
(Multiple Choice)
4.8/5  (28)
(28)
Determine the solution to the system of inequalities.
- x\geq0 y\geq0 2x+2y\leq4 3x+y\leq5
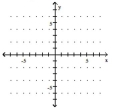
(Multiple Choice)
4.9/5  (35)
(35)
Solve the problem.
-The sum of the measures of the angles of a triangle is 180°. The smallest angle of the triangle has a measuree the measure of the second smallest angle. The largest angle is 9° less than eleven times the measure of the second smallest angle. Determine the measure of each angle.
(Multiple Choice)
4.8/5  (35)
(35)
Determine the solution to the system of equations graphically. If the system is inconsistent or dependent, so state.
- y=-3x-1 -6x-2y=2
(Multiple Choice)
4.8/5  (34)
(34)
Solve the system of equations using determinants.
- -4x-2y=-18 -8x=-20+4y
(Multiple Choice)
4.9/5  (31)
(31)
Determine the solution to the system of inequalities.
- |y|>6 y\leqx-3

(Multiple Choice)
4.8/5  (45)
(45)
Determine the solution to the system of equations graphically. If the system is inconsistent or dependent, so state.
- y=-9x y=9x-18
(Multiple Choice)
4.9/5  (41)
(41)
Solve the problem.
-Three solutions to the equation Ax + By + Cz = 14 are (5, -4, 1), (1, 3, 0), and (3, 1, -4). Determine the values of A, B, and C and write the equation using the numerical values found.
(Multiple Choice)
4.9/5  (33)
(33)
Write each equation in slope-intercept form. Without graphing the equations, state whether the system of equations is
consistent, inconsistent, or dependent. Also indicate whether the system has exactly one solution, no solution, or an
infinite number of solutions.
- x+3y=3 8x-5y=-5
(Multiple Choice)
4.9/5  (43)
(43)
Solve the system of equations using the addition method.
- x-y+2z=3 5x+z=0 x+5y+z=-15
(Multiple Choice)
4.9/5  (36)
(36)
Determine whether the system is inconsistent, dependent, or neither.
- x-y+2z=-2 4x+z=0 -x+y-2z=4
(Multiple Choice)
4.8/5  (44)
(44)
Solve the problem.
-The Little Town Arts Center charges $22 for adults, $18 for senior citizens, and $7 for children under 12 for their live performances on Sunday afternoon. This past Sunday, the paid revenue was $11,615 for 755 tickets sold.
There were 44 more children than adults. How many children attended?
(Multiple Choice)
4.8/5  (30)
(30)
Determine the solution to the system of inequalities.
- y\geq1 |x|>5
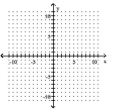
(Multiple Choice)
4.9/5  (42)
(42)
Find the solution to the system of equations by substitution.
- x+6y=-45 -6x+5y=-17
(Multiple Choice)
4.8/5  (35)
(35)
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use
the information in the figure to answer the question. 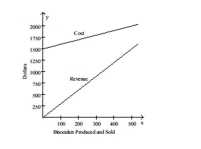 -The company's cost for manufacturing x binoculars is determined by the equation y = x + 1500. The revenue for selling x binoculars is determined by the equation y = 3x. The break-even point is the point at which the cost
And revenue equations intersect. How many binoculars must be produced and sold for the company to break
Even?
-The company's cost for manufacturing x binoculars is determined by the equation y = x + 1500. The revenue for selling x binoculars is determined by the equation y = 3x. The break-even point is the point at which the cost
And revenue equations intersect. How many binoculars must be produced and sold for the company to break
Even?
(Multiple Choice)
4.7/5  (39)
(39)
Showing 81 - 100 of 116
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)