Exam 4: Systems of Equations and Inequalities
Exam 1: Basic Concepts306 Questions
Exam 2: Equations and Inequalities234 Questions
Exam 3: Graphs and Functions61 Questions
Exam 4: Systems of Equations and Inequalities116 Questions
Exam 5: Polynomials and Polynomial Functions112 Questions
Exam 6: Rational Expressions and Equations130 Questions
Exam 7: Roots, Radicals, and Complex Numbers298 Questions
Exam 8: Quadratic Functions221 Questions
Exam 9: Exponential and Logarithmic Functions229 Questions
Exam 10: Characteristics of Functions and Their Graphs142 Questions
Exam 11: Conic Sections132 Questions
Exam 12: Sequences, Series, and Probability208 Questions
Select questions type
Determine the solution to the system of inequalities.
- |x|<5 |y|<3
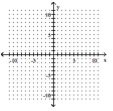
(Multiple Choice)
4.8/5  (33)
(33)
Determine whether the system is inconsistent, dependent, or neither.
- 2x+y=-1 3y-4z=-25 2x+4y-4z=-26
(Multiple Choice)
4.8/5  (33)
(33)
Solve the system of equations using the addition method.
- 3x+5y+z=1 5x-2y-z=33 5x+y+3z=11
(Multiple Choice)
4.9/5  (44)
(44)
Find the solution to the system of equations by substitution.
- x+2y=2 7x-6y=-6
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-Three planes intersect as illustrated below. Is the system consistent, inconsistent, or dependent? 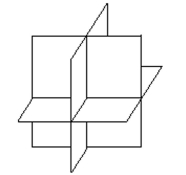
(Multiple Choice)
4.8/5  (42)
(42)
Solve the system of equations using the addition method.
- x+y=-2 2x+2y+4z=16 x-z=-9
(Multiple Choice)
4.7/5  (42)
(42)
Solve the system of equations using the addition method.
- 4x-4y=2 -8x+8y=-8
(Multiple Choice)
4.8/5  (40)
(40)
Determine the solution to the system of inequalities.
- x\geq0 y\geq0 x+y\leq6 10x+5y\leq50 5x+10y\leq50
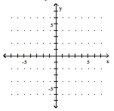
(Multiple Choice)
4.8/5  (34)
(34)
Solve the system of equations using the addition method.
- 2x+8y =-42 12x+2y =70
(Multiple Choice)
4.8/5  (36)
(36)
The figure shows the graphs of the cost and revenue functions for a company that manufactures and sells binoculars. Use
the information in the figure to answer the question. 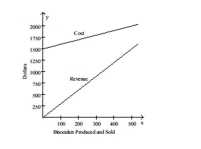 -The company's cost for manufacturing x binoculars is determined by the equation y = x + 1500. The revenue for selling x binoculars is determined by the equation y = 3x. The break-even point is the point at which the cost
And revenue equations intersect. At the break-even point both cost and revenue are what?
-The company's cost for manufacturing x binoculars is determined by the equation y = x + 1500. The revenue for selling x binoculars is determined by the equation y = 3x. The break-even point is the point at which the cost
And revenue equations intersect. At the break-even point both cost and revenue are what?
(Multiple Choice)
4.7/5  (46)
(46)
Solve the problem.
-A chemist needs 140 milliliters of a 70% solution but has only 66% and 94% solutions available. Find how many milliliters of each that should be mixed to get the desired solution.
(Multiple Choice)
4.9/5  (45)
(45)
Solve the system of equations using the addition method.
- x-y+z=-3 x+y+z=-5 x+y-z=5
(Multiple Choice)
4.9/5  (41)
(41)
Solve the system using determinants.
- 4x+3y-2z=7 -3y+2z=5 -4x+3z=0
(Multiple Choice)
4.8/5  (44)
(44)
Solve the system using determinants.
- 3x+4y-z=42 x-4y+5z=-2 2x+y+z=23
(Multiple Choice)
4.8/5  (36)
(36)
Find the solution to the system of equations by substitution.
- 7x+y=0 -7x+y=-14
(Multiple Choice)
4.8/5  (40)
(40)
Solve the problem.
-A ceramics workshop makes serving bowls, platters, and bread baskets to sell at its Winter Festival. A serving bowl takes 3 hours to prepare, 2 hours to paint, and 8 hours to fire. A platter takes 15 hours to prepare, 3 hours
To paint, and 4 hours to fire. A bread basket takes 4 hours to prepare, 14 hours to paint, and 7 hours to fire. If the
Workshop has 101 hours for prep time, 55 hours for painting, and 82 hours for firing, how many of each can be
Made?
(Multiple Choice)
4.9/5  (39)
(39)
Write each equation in slope-intercept form. Without graphing the equations, state whether the system of equations is
consistent, inconsistent, or dependent. Also indicate whether the system has exactly one solution, no solution, or an
infinite number of solutions.
- 2x-6y=5 -8x+24y=-15
(Multiple Choice)
4.9/5  (36)
(36)
Determine the solution to the system of inequalities.
- x\geq0 y\geq0 x+y\leq4 6x+2y\leq12
(Multiple Choice)
4.7/5  (36)
(36)
Showing 21 - 40 of 116
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)