Exam 4: Graphing and Optimization
Exam 1: Functions and Graphs71 Questions
Exam 2: Limits and the Derivative188 Questions
Exam 3: Additional Derivative Topics98 Questions
Exam 4: Graphing and Optimization126 Questions
Exam 5: Integration38 Questions
Exam 7: Multivariable Calculus92 Questions
Exam 8: Appendix A: Basic Algebra Review44 Questions
Exam 9: Appendix B: Special Topics Online at Googlmjbxrg20 Questions
Select questions type
Write the word or phrase that best completes each statement or answers the question.
-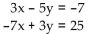
(Multiple Choice)
4.9/5  (26)
(26)
Provide an appropriate response.
-Only one of the following augmented matrices of a linear system is in a reduced form. Choose the matrix that is in reduced form.
(Multiple Choice)
4.9/5  (38)
(38)
Provide an appropriate response.
-Determine the value of each variable. 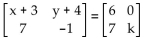
(Multiple Choice)
4.8/5  (34)
(34)
Solve the equation for the indicated variable. Assume that the dimensions are such that matrix multiplication and
addition are possible and that inverses exist when needed.
-Solve for Y: XY + ZY = A
(Multiple Choice)
4.8/5  (40)
(40)
Provide an appropriate response.
-Given matrices M = 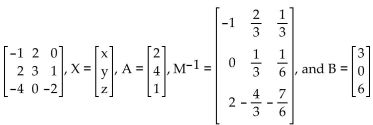 solve the matrix equations
MX = A and MX = B.
solve the matrix equations
MX = A and MX = B.
(Essay)
4.8/5  (42)
(42)
Write the word or phrase that best completes each statement or answers the question.
-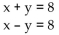
(Multiple Choice)
4.7/5  (37)
(37)
Find the system of equations to model the problem. DO NOT SOLVE THIS SYSTEM.
-Labor and material costs for manufacturing each of three types of products M, N, and P are given in the table:
Product  The weekly allocation for labor is $50,000 and for materials is $80,000. There are to be 3 times as many units of product
M manufactured as units of product P. How many of each type of product would be manufactured each week to use
exactly each of the weekly allocations? Set up a system of linear equations, letting x1, x2, and x3 be the number
of units of products M, N, and P, respectively, manufactured in one week.
The weekly allocation for labor is $50,000 and for materials is $80,000. There are to be 3 times as many units of product
M manufactured as units of product P. How many of each type of product would be manufactured each week to use
exactly each of the weekly allocations? Set up a system of linear equations, letting x1, x2, and x3 be the number
of units of products M, N, and P, respectively, manufactured in one week.
(Essay)
4.9/5  (35)
(35)
Perform the indicated row operations on the following matrix.  -
-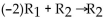
(Multiple Choice)
4.9/5  (40)
(40)
Perform the operation, if possible.
-If a and b are nonzero real numbers and A = 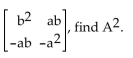
(Essay)
4.7/5  (39)
(39)
Solve the problem.
-Daisy has a desk full of quarters and nickels. If she has a total of 23 coins with a total face value of $4.35, how many of the coins are nickels?
(Multiple Choice)
4.8/5  (40)
(40)
Perform the operation, if possible.
-A = 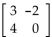 , B , B =
, B , B = 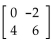 Find AB.
Find AB.
(Multiple Choice)
4.8/5  (35)
(35)
Solve the problem.
-A supermarket chain sells oranges, apples, peaches, and bananas in three stores located throughout a large
metropolitan area. The average number of pounds sold per day in each store is summarized in matrix M. "In
season" and "out of season" prices, per pound, of each fruit are given in matrix N. What is the total, for the three
stores, of "in season" daily revenue for the four fruits? The "out of season" peach sales represent what percentage of
the daily total "out of season" revenues for store 3? 
(Short Answer)
4.8/5  (42)
(42)
Solve the problem.
-Two sectors of a textbook economy are (1) communication equipment and (2) components and accessories. In 2005 the input-output table involving these two sectors was as follows. 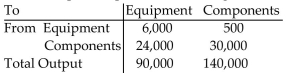 Determine the production levels necessary in these two sectors to meet a demand for $80,000 of equipment and $90,000
Of components. Round to significant digits.
Determine the production levels necessary in these two sectors to meet a demand for $80,000 of equipment and $90,000
Of components. Round to significant digits.
(Multiple Choice)
4.9/5  (39)
(39)
Solve the system as matrix equations using inverses.
-There were 340 people at a play. The admission price was $2 for adults and $1 for children. The admission receipts were $490. How many adults and how many children attended?
(Multiple Choice)
4.9/5  (37)
(37)
Solve the problem.
-A large oil company produces three grades of gasoline: regular, unleaded, and super-unleaded. To produce
these gasolines, equipment is used which requires as input certain amounts of each of the three grades of
gasoline. To produce a dollar's worth of regular requires inputs of $0.14 worth of regular, $0.18 worth of
unleaded, and $0.17 worth of super-unleaded. To produce a dollar's worth of unleaded requires inputs of $0.14
worth of regular, $0.15 worth of unleaded, and $0.13 worth of super-unleaded. To produce a dollar's worth of
super-unleaded requires inputs of $0.15 worth of regular, $0.17 worth of unleaded, and $0.11 worth of
super-unleaded. In addition, the oil company has final demands for each of the different grades of gasoline.
Find the technology matrix that would be used in determining the total output of each grade of gasoline.
(Essay)
4.8/5  (42)
(42)
Provide an appropriate response.
-Write the augmented matrix for the system. 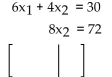
(Multiple Choice)
4.8/5  (34)
(34)
Write the matrix equation as a system of linear equations without matrices.
-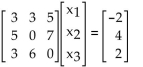
(Multiple Choice)
4.8/5  (46)
(46)
Find the matrix product mentally, without the use of a calculator or pencil-and-paper calculations.
-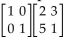
(Multiple Choice)
5.0/5  (28)
(28)
Solve the problem.
-A chain of amusement parks pays experienced workers $240 per week and inexperienced workers $220 per week. The
total number of workers and total weekly wages at three different parks are given in the table. How many experienced
workers does each park employ? Set up a system of linear equations and solve using matrix inverse methods. 
(Essay)
4.8/5  (35)
(35)
Showing 21 - 40 of 126
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)