Exam 4: Graphing and Optimization
Exam 1: Functions and Graphs71 Questions
Exam 2: Limits and the Derivative188 Questions
Exam 3: Additional Derivative Topics98 Questions
Exam 4: Graphing and Optimization126 Questions
Exam 5: Integration38 Questions
Exam 7: Multivariable Calculus92 Questions
Exam 8: Appendix A: Basic Algebra Review44 Questions
Exam 9: Appendix B: Special Topics Online at Googlmjbxrg20 Questions
Select questions type
The system cannot be solved by matrix inverse methods. Find a method that could be used and then solve the system.
-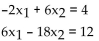
(Multiple Choice)
4.8/5  (36)
(36)
Solve the problem.
-A trucking firm wants to purchase 10 trucks that will provide exactly 28 tons of additional shipping capacity. A
model A truck holds 2 tons, a model B truck holds 3 tons, and a model C truck holds 5 tons. How many trucks
of each model should the company purchase to provide the additional shipping capacity? Set up a system of
linear equations and solve using Gauss-Jordan elimination. There may be more than one solution.
(Essay)
4.7/5  (28)
(28)
Find the values of a, b, c, and d that make the matrix equation true.
-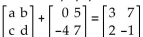
(Multiple Choice)
4.9/5  (38)
(38)
Solve the system mentally, without the use of a calculator or pencil-and-paper calculation. Try to visualize the graphs of
both lines.
-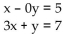
(Multiple Choice)
4.7/5  (42)
(42)
Provide an appropriate response.
-Use the matrix method on a graphing calculator to solve the system 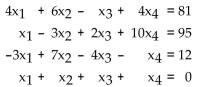 Carry values to two decimal places.
Carry values to two decimal places.
(Essay)
4.9/5  (35)
(35)
Solve the problem.
-Suppose that the supply and demand equations for a logo sweat shirt in a particular week are eek are 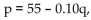 for fo
the demand equation; and d
for fo
the demand equation; and d 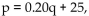 , for the supply equation. Find the equilibrium price and quantit for the supply equation. Find the equilibrium price and quantiy.
, for the supply equation. Find the equilibrium price and quantit for the supply equation. Find the equilibrium price and quantiy.
(Essay)
4.8/5  (30)
(30)
Perform the indicated operations given the matrices.
-Let A = 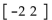 an ad B =
an ad B = 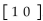 ;; 2A + 3B
;; 2A + 3B
(Multiple Choice)
5.0/5  (36)
(36)
Perform the indicated operations given the matrices.
-Let A = 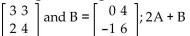
(Multiple Choice)
4.8/5  (39)
(39)
Solve the problem.
-A company makes three chocolate candies: cherry, almond, and raisin. Matrix A gives the number of units of each ingredient in each type of candy in one batch. Matrix B gives the cost of each ingredient (dollars per unit)
From suppliers X and Y. What is the cost of 100 batches from supplier X? 
(Multiple Choice)
4.7/5  (36)
(36)
Use the given encoding matrix A to solve the problem.
-Use the given message to construct the code matrix by assigning numbers to the letters and symbols. Use the numerical assignment a = 1, b = 2, . . . , z = 26, space = 30, period = 40, and apostrophe = 60.
Message: CALL ME TOMORROW.
Encoding matrix A == 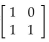
(Multiple Choice)
5.0/5  (41)
(41)
Solve the equation for the indicated variable. Assume that the dimensions are such that matrix multiplication and
addition are possible and that inverses exist when needed.
-Solve for A: AY - A = B
(Multiple Choice)
4.8/5  (36)
(36)
User row operations to change the matrix to reduced form.
-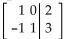
(Multiple Choice)
4.9/5  (40)
(40)
Find the system of equations to model the problem. DO NOT SOLVE THIS SYSTEM.
-There were 35,000 people at a ball game in Atlanta. The day's receipts were $290,000. How many people paid $14 for reserved seats and how many paid $6 for general admission? Let x represent the number of reserved
Seats and y represent the number of general admission seats.
(Multiple Choice)
4.8/5  (36)
(36)
Write the system as a matrix equation of the form AX = B.
-6 8 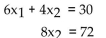
(Multiple Choice)
4.8/5  (34)
(34)
Write the linear system corresponding to the reduced augmented matrix.
-
(Multiple Choice)
4.8/5  (35)
(35)
Provide an appropriate response.
-Solve the linear system corresponding to the following augmented matrix: 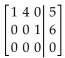
(Essay)
4.8/5  (36)
(36)
The matrix is the final matrix form for a system of two linear equations in variables x1 and x2. Write the Solution of the
system.
-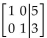
(Multiple Choice)
4.8/5  (38)
(38)
Showing 81 - 100 of 126
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)