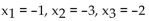Exam 4: Graphing and Optimization
Exam 1: Functions and Graphs71 Questions
Exam 2: Limits and the Derivative188 Questions
Exam 3: Additional Derivative Topics98 Questions
Exam 4: Graphing and Optimization126 Questions
Exam 5: Integration38 Questions
Exam 7: Multivariable Calculus92 Questions
Exam 8: Appendix A: Basic Algebra Review44 Questions
Exam 9: Appendix B: Special Topics Online at Googlmjbxrg20 Questions
Select questions type
State whether the matrix is in reduced form or not in reduced form.
-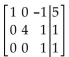
Free
(Multiple Choice)
4.8/5  (30)
(30)
Correct Answer:
A
Perform the operation, if possible.
-A = 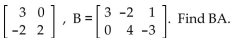
Free
(Multiple Choice)
4.7/5  (32)
(32)
Correct Answer:
B
Find the system of equations to model the problem. DO NOT SOLVE THIS SYSTEM.
-In producing three types of bricks: face bricks, common bricks, and refractory bricks, a factory incurs labor,
material, and utility costs. To produce one pallet of face bricks, the labor, material, and utility costs are $50, $75,
and $35, respectively. To produce one pallet of common bricks, the labor, material, and utility costs are $50, $60,
and $30, respectively, while the corresponding costs for refractory bricks are $75, $100, and $45. In a certain
month the company has allocated $12,000 for labor costs, $14,500 for material costs and $6,000 for utility costs.
How many pallets of each type of brick should be produced in that month to exactly utilize these allocations?
Set up a system of linear equations, letting x, y, and z be the number of pallets of face, common, and refractory
bricks, respectively, that must be produced in that month.
(Essay)
4.7/5  (31)
(31)
Find the values of a, b, c, and d that make the matrix equation true.
-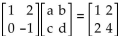
(Multiple Choice)
4.7/5  (30)
(30)
Solve the system as matrix equations using inverses.
-A company produces three models of MP3 players, models A, B, and C. Each model A machine requires 3.2 hours of electronics work, 2.8 hours of assembly time, and 4.4 hours of quality assurance time. Each model B
Machine requires 5.4 hours of electronics work, 2.4 hours of assembly time, and 3.4 hours of quality assurance
Time. Each model C machine requires 2.2 hours of electronics work, 5.8 hours of assembly time, and 4.8 hours of
Quality assurance time. There are 303 hours available each week for electronics, 393 hours for assembly, and
416 hours for quality assurance. How many of each model should be produced each week if all available time
Must be used?
(Multiple Choice)
4.7/5  (40)
(40)
Solve the problem.
-A textbook economy has only two industries, the electric company and the gas company. Each dollar's worth of the electric company's output requires 0.20 of its own output and 0.4 of the gas company's output. Each dollar's
Worth of the gas company's output requires 0.50 of its own output and 0.7 of the electric company's output.
What should the production of electricity and gas be (in dollars) if there is a $16 M demand for electricity and a $7
M demand for gas?
(Multiple Choice)
4.9/5  (41)
(41)
Write the system as a matrix equation of the form AX = B.
-8 4 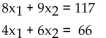
(Multiple Choice)
4.9/5  (34)
(34)
Solve the problem.
-The input-output matrix for an economy is TT  Find the internal consumption.
Find the internal consumption.
(Multiple Choice)
4.7/5  (41)
(41)
Solve the problem.
-A retail company offers, through two different stores in a city, three models, A, B, and C, of a particular brand of
camping stove. The inventory of each model on hand in each store is summarized in matrix M. Wholesale (W)
and retail (R) prices of each model are summarized in matrix M. Find the product MN and label its columns and
rows appropriately. What is the wholesale value of the inventory in Store 1? 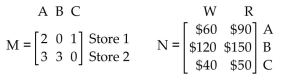
(Essay)
4.9/5  (30)
(30)
Find the system of equations to model the problem. DO NOT SOLVE THIS SYSTEM.
-A paper company produces high, medium, and low grade paper. The number of tons of each grade that is produced
from one ton of pulp depends on the source of that pulp. The following table lists three sources and the amount of each
grade of paper that can be made for one ton of pulp from each source. 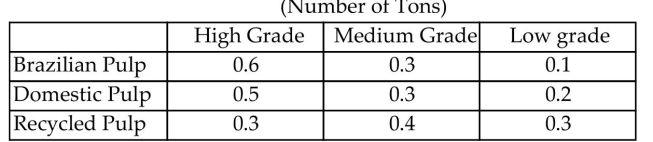 The paper company has orders for 11 tons of high grade, 15 tons of medium grade, and 14 tons of low grade paper.
How many tons of each type of pulp should be used to fill these orders exactly? Set up a system of linear equations,
letting x, y, and z be the number of tons of Brazilian pulp, domestic pulp, and recycled pulp, respectively, needed to fill
the orders.
The paper company has orders for 11 tons of high grade, 15 tons of medium grade, and 14 tons of low grade paper.
How many tons of each type of pulp should be used to fill these orders exactly? Set up a system of linear equations,
letting x, y, and z be the number of tons of Brazilian pulp, domestic pulp, and recycled pulp, respectively, needed to fill
the orders.
(Essay)
4.9/5  (36)
(36)
The matrix is the final matrix form for a system of two linear equations in variables x1 and x2. Write the Solution of the
system.
-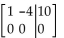
(Multiple Choice)
4.9/5  (32)
(32)
Identify the row operation that produces the resulting matrix.
-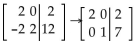
(Multiple Choice)
4.8/5  (32)
(32)
Provide an appropriate response.
-Solve the matrix equation uation 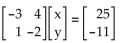 by using the inverse of the coefficient matrix. Also, solve the system if the constants 25 and -11 are replaced by 1 and
3, respectively.
by using the inverse of the coefficient matrix. Also, solve the system if the constants 25 and -11 are replaced by 1 and
3, respectively.
(Essay)
4.9/5  (44)
(44)
Showing 1 - 20 of 126
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)