Exam 1: Functions and Graphs
Exam 1: Functions and Graphs71 Questions
Exam 2: Limits and the Derivative188 Questions
Exam 3: Additional Derivative Topics98 Questions
Exam 4: Graphing and Optimization126 Questions
Exam 5: Integration38 Questions
Exam 7: Multivariable Calculus92 Questions
Exam 8: Appendix A: Basic Algebra Review44 Questions
Exam 9: Appendix B: Special Topics Online at Googlmjbxrg20 Questions
Select questions type
Solve the problem.
-Find the Celsius temperature (to the nearest degree) when Fahrenheit temperature is 95 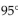 ° by solving the equation 95 =
° by solving the equation 95 = 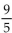 CC + 32, where F is the Fahrenheit temperature (in degrees) and C is the Celsius temperature.
CC + 32, where F is the Fahrenheit temperature (in degrees) and C is the Celsius temperature.
(Multiple Choice)
4.8/5  (39)
(39)
Provide an appropriate response.
-Find the line passing through the two points. Write the equation in standard form. (-3, 6) and (6, 6)
(Multiple Choice)
5.0/5  (37)
(37)
Provide an appropriate response.
-Use the graph to find the slope-intercept form of the equation of the line. 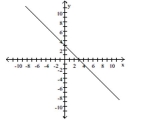
(Multiple Choice)
4.7/5  (32)
(32)
Provide an appropriate response.
-Write the equation of a line that passes through (-1, 4) and (5, -1). Write the final answer in the form Ax + By = C where A, B, and C are integers with no common divisors (other than ±1) and A > 0.
(Multiple Choice)
4.8/5  (26)
(26)
Solve the inequality and graph. Express your answer in interval notation.
-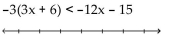
(Multiple Choice)
4.9/5  (28)
(28)
Solve the problem. Express your answer as an integer or simplified fraction.
-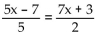
(Multiple Choice)
4.8/5  (33)
(33)
Use the REGRESSION feature on a graphing calculator.
-The use of bottled water in the United States has shown a steady increase in recent years. The table shows the annual per capita consumption for the years 1995 - 2001. 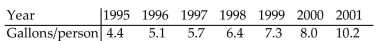 With x being the years since 1995, find the linear function that represents this data. Round your answer to two decimal
Places.
With x being the years since 1995, find the linear function that represents this data. Round your answer to two decimal
Places.
(Multiple Choice)
4.9/5  (32)
(32)
Provide an appropriate response.
-Find the standard form of the equation of the line with slope of 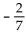 and passing through (4, 4).
and passing through (4, 4).
(Multiple Choice)
4.8/5  (30)
(30)
Provide an appropriate response.
-Use the graph to find the slope, x-intercept and y-intercept of the line. 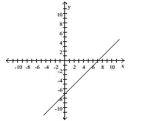
(Multiple Choice)
5.0/5  (38)
(38)
Solve the formula for the specified variable.
-F = 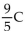 + 32 for C
+ 32 for C
(Multiple Choice)
4.9/5  (30)
(30)
Find the slope and y intercept of the graph of the equation.
-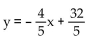
(Multiple Choice)
4.9/5  (35)
(35)
Provide an appropriate response.
-Graph the linear function defined by ion defined by f(x) 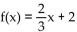 2 and indicate the slope and intercepts.
2 and indicate the slope and intercepts. 
(Multiple Choice)
4.8/5  (40)
(40)
Find the slope and y intercept of the graph of the equation.
-y = -4x + 6
(Multiple Choice)
4.9/5  (38)
(38)
Solve the problem. Express your answer as an integer or simplified fraction.
-Solve: : 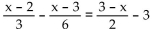
(Multiple Choice)
4.7/5  (29)
(29)
Provide an appropriate response.
-Write the equation of a line that passes through (3, 9) and (0, -7). Write the final answer in the form Ax + By = C where A, B, and C are integers with no common divisors (other than ±1) and A > 0.
(Multiple Choice)
4.9/5  (35)
(35)
Solve the inequality and graph. Express your answer in interval notation.
-7x - 3 > 6x - 6 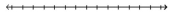
(Multiple Choice)
4.9/5  (36)
(36)
Write an equation of the line with the indicated slope and y intercept.
-Slope = 4, y intercept = -5
(Multiple Choice)
5.0/5  (35)
(35)
Provide an appropriate response.
-Find the line passing through the two points. Write the equation in standard form. (10, 9) and (10, 1)
(Multiple Choice)
4.8/5  (29)
(29)
Find the slope of the line containing the given points.
-(6, 1) and (6, - 4)
(Multiple Choice)
4.7/5  (30)
(30)
Solve the problem.
-At a local grocery store the demand for ground beef is approximately 50 pounds per week when the price per pound is $4, but is only 40 pounds per week when the price rises to $5.50 per pound. Assuming a linear
Relationship between the demand x and the price per pound p, express the price as a function of demand. Use
This model to predict the demand if the price rises to $5.80 per pound.
(Multiple Choice)
4.8/5  (35)
(35)
Showing 41 - 60 of 71
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)