Exam 3: Differentiation Rules
Exam 1: Functions and Models160 Questions
Exam 2: Limits and Derivatives160 Questions
Exam 3: Differentiation Rules160 Questions
Exam 4: Applications of Differentiation159 Questions
Exam 5: Integrals160 Questions
Exam 6: Applications of Integration160 Questions
Exam 7: Techniques of Integration160 Questions
Exam 8: Further Applications of Integration160 Questions
Exam 9: Differential Equations160 Questions
Exam 10: Parametric Equations and Polar Coordinates160 Questions
Exam 11: Infinite Sequences and Series160 Questions
Exam 12: Vectors and the Geometry of Space159 Questions
Exam 13: Vector Functions160 Questions
Exam 14: Partial Derivatives158 Questions
Exam 15: Multiple Integrals160 Questions
Exam 16: Vector Calculus160 Questions
Exam 17: Second-Order Differential Equations160 Questions
Select questions type
A circle's radius is increasing.Find the rate of change of the area of the circle with respect to the radius 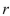 when
when 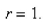
(Essay)
4.8/5  (39)
(39)
Find an equation of the tangent line to the curve 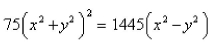 at the point (4,1).Select the correct Answer
at the point (4,1).Select the correct Answer
(Multiple Choice)
4.7/5  (47)
(47)
Select the correct Answer: for each question.
-Find 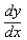 by implicit differentiation.
by implicit differentiation. 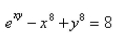
(Multiple Choice)
4.7/5  (35)
(35)
If a tank holds 5000 gallons of water, and that water can drain from the tank in 40 minutes, then Torricelli's Law gives the volume 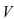 of water remaining in the tank after
of water remaining in the tank after 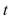 minutes as
minutes as 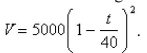 Find the rate at which water is draining from the tank after
Find the rate at which water is draining from the tank after 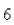 minutes.
minutes.
(Essay)
4.8/5  (41)
(41)
A baseball diamond is a square with side 90 ft.A ba 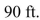 tter hits the ball and runs toward first base with a speed of
tter hits the ball and runs toward first base with a speed of 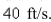 At what rate is his distance from second base decreasing when he is halfway to first base? Round the result to the nearest hundredth.
At what rate is his distance from second base decreasing when he is halfway to first base? Round the result to the nearest hundredth.
(Essay)
4.8/5  (36)
(36)
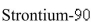 has a half-life of
has a half-life of 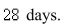 A sample has a mass of
A sample has a mass of 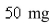 initially.Find the mass remaining after 42 days.
initially.Find the mass remaining after 42 days.
(Essay)
4.8/5  (40)
(40)
Select the correct Answer: for each question.
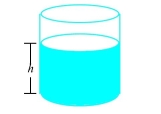
-Water flows from a tank of constant cross-sectional area 50 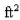 through an orifice of constant cross-sectional area
through an orifice of constant cross-sectional area 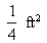 located at the bottom of the tank.Initially, the height of the water in the tank was 20 ft, and t sec later it was given by the equation
located at the bottom of the tank.Initially, the height of the water in the tank was 20 ft, and t sec later it was given by the equation 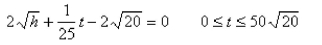 How fast was the height of the water decreasing when its height was 2 ft?
How fast was the height of the water decreasing when its height was 2 ft? 
(Multiple Choice)
4.7/5  (30)
(30)
Select the correct Answer for each question.
-Suppose that 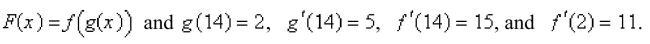 Find
Find 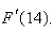
(Multiple Choice)
4.7/5  (36)
(36)
Gravel is being dumped from a conveyor belt at a rate of 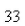 ft/min and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal.How fast is the height of the pile increasing when the pile is
ft/min and its coarseness is such that it forms a pile in the shape of a cone whose base diameter and height are always equal.How fast is the height of the pile increasing when the pile is 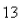 ft high? Round the result to the nearest hundredth.Select the correct Answer
ft high? Round the result to the nearest hundredth.Select the correct Answer 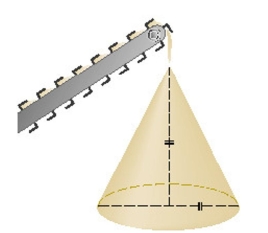
(Multiple Choice)
4.9/5  (38)
(38)
Refer to the law of laminar flow.Consider a blood vessel with radius 0.01 cm, length 3 cm, pressure difference 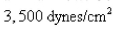 and viscosity
and viscosity 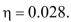 Find the velocity of the blood at radius
Find the velocity of the blood at radius 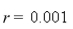
(Essay)
4.9/5  (36)
(36)
The half-life of 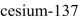 is 30 years.Suppose we have a
is 30 years.Suppose we have a 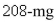 sample.Find the mass that remains after
sample.Find the mass that remains after 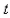 years.Select the correct Answer
years.Select the correct Answer
(Multiple Choice)
4.7/5  (35)
(35)
Showing 141 - 160 of 160
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)