Exam 6: Exponential and Logarithmic Functions
Exam 1: Equations and Inequalities365 Questions
Exam 2: Graphs83 Questions
Exam 3: Functions and Their Graphs112 Questions
Exam 4: Linear and Quadratic Functions21 Questions
Exam 5: Polynomial and Rational Functions45 Questions
Exam 6: Exponential and Logarithmic Functions234 Questions
Exam 7: Analytic Geometry129 Questions
Exam 8: Systems of Equations and Inequalities428 Questions
Exam 9: Sequences; Induction; the Binomial Theorem242 Questions
Exam 10: Counting and Probability110 Questions
Exam 11: Graphing Utilities25 Questions
Select questions type
For the given functions f and g, find the requested composite function value.
-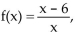 g(x)=
g(x)= 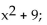 Find (g ∘ f)(-2).
Find (g ∘ f)(-2).
(Multiple Choice)
4.8/5  (26)
(26)
Change the exponential expression to an equivalent expression involving a logarithm.
-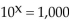
(Multiple Choice)
4.8/5  (47)
(47)
Decide whether or not the functions are inverses of each other.
-f(x)= 4x + 16, g(x)= 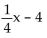
(Multiple Choice)
4.7/5  (40)
(40)
Use a calculator to evaluate the expression. Round your answer to three decimal places
-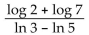
(Multiple Choice)
5.0/5  (32)
(32)
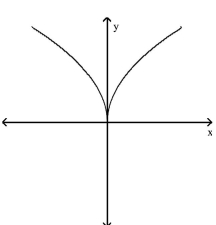
Use the horizontal line test to determine whether the function is one -to-one.
-
(Multiple Choice)
4.9/5  (35)
(35)
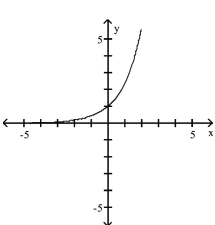
The graph of an exponential function is given. Match the graph to one of the following functions.
-
(Multiple Choice)
4.8/5  (36)
(36)
Indicate whether the function is one-to-one.
-{(-10, 4), (-15, 4), (-16, 1)}
(Multiple Choice)
4.7/5  (35)
(35)
Decide whether the composite functions, f ∘ g and g ∘ f, are equal to x.
-f(x)= 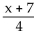 , g(x)= 4x - 7
, g(x)= 4x - 7
(Multiple Choice)
4.7/5  (24)
(24)
For the given functions f and g, find the requested composite function.
-f(x)= x 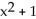 , g(x)=
, g(x)= 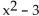 ; Find (f ∘ g)(x).
; Find (f ∘ g)(x).
(Multiple Choice)
4.9/5  (27)
(27)
Decide whether the composite functions, f ∘ g and g ∘ f, are equal to x.
-f(x)= 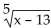 , g(x)=
, g(x)= 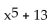
(Multiple Choice)
4.9/5  (40)
(40)
Change the logarithmic expression to an equivalent expression involving an exponent.
-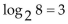
(Multiple Choice)
4.8/5  (37)
(37)
Showing 181 - 200 of 234
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)