Exam 9: Trigonometric Models
Exam 1: Functions and Linear Models100 Questions
Exam 2: Nonlinear Functions and Models88 Questions
Exam 3: Introduction to the Derivative140 Questions
Exam 4: Techniques of Differentiation With Applications106 Questions
Exam 5: Further Applications of the Derivative85 Questions
Exam 6: The Integral71 Questions
Exam 7: Further Integration Techniques and Applications of the Integral117 Questions
Exam 8: Functions of Several Variables133 Questions
Exam 9: Trigonometric Models66 Questions
Select questions type
The depth of water 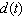 at my favorite surfing spot varies from 5 to 15 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model to the depth of water as a function of time t in hours since midnight in Sunday morning.
at my favorite surfing spot varies from 5 to 15 feet, depending on the time. Last Sunday high tide occurred at 5:00 A.M. and the next high tide occurred at 6:30 P.M. Use a sine function to model to the depth of water as a function of time t in hours since midnight in Sunday morning.
(Essay)
4.9/5  (35)
(35)
Recall that the average of a function 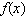 on an interval
on an interval 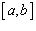 is
is 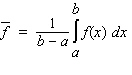 Calculate the 2-unit moving average of the function.
Calculate the 2-unit moving average of the function. 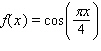
(Multiple Choice)
4.8/5  (33)
(33)
Model the curve with a sine function. 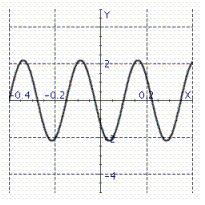 Note that the period of the curve is
Note that the period of the curve is 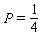 and its range is 2.2, 2.2 and the graph of the sine function is shifted to the left 0.9 units.
and its range is 2.2, 2.2 and the graph of the sine function is shifted to the left 0.9 units.
(Multiple Choice)
4.9/5  (31)
(31)
Model the curve with a sine function. 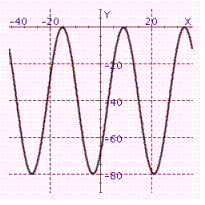 Note that the period of the curve is
Note that the period of the curve is 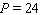 and its range is
and its range is 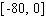 , the graph of the sine function is shifted to the right 3 units.
, the graph of the sine function is shifted to the right 3 units.
(Multiple Choice)
4.7/5  (29)
(29)
Model the curve with a cosine function. 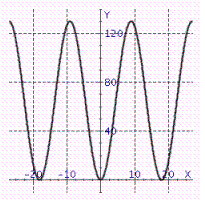 Note that the period of the curve is
Note that the period of the curve is 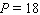 , its range is
, its range is 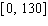 and the graph of the cosine function is shifted upward 65 units and shifted to the right 9 units. Write the model function as a function of (x)and
and the graph of the cosine function is shifted upward 65 units and shifted to the right 9 units. Write the model function as a function of (x)and 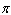 .
.
(Essay)
4.9/5  (43)
(43)
Sales of computers are subject to seasonal fluctuations. Computer City s sales of computers in 1995 and 1996 can be approximated by the function 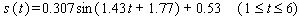 where
where 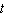 is time in quarters
is time in quarters 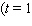 represents the end of the first quarter of 1995)and
represents the end of the first quarter of 1995)and 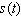 is computer sales (quarterly revenue)in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales. Maximum sales __________ billions of dollars Minimum sales __________ billions of dollars
is computer sales (quarterly revenue)in billions of dollars. Estimate Computer City s maximum and minimum quarterly revenue from computer sales. Maximum sales __________ billions of dollars Minimum sales __________ billions of dollars
(Essay)
4.9/5  (43)
(43)
Use the conversion formula 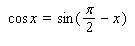 to replace the expression
to replace the expression 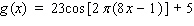 by a sine function.
by a sine function.
(Multiple Choice)
4.8/5  (42)
(42)
Starting with the identity 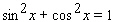 , choose the right trigonometric identity.
, choose the right trigonometric identity.
(Multiple Choice)
4.7/5  (37)
(37)
Use the addition formulas: sin ( x + y )= sin x cos y + cos x sin y sin ( x - y )= sin x cos y - cos x sin y cos ( x + y )= cos x cos y - sin x sin y cos ( x - y )= cos x cos y + sin x sin y to express 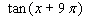 in terms of
in terms of 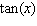 .
.
(Multiple Choice)
5.0/5  (34)
(34)
Model the curve with a cosine function. 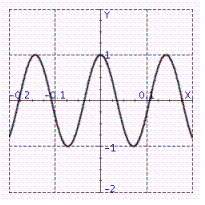 Note that the period of the curve is
Note that the period of the curve is 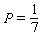 and its range is
and its range is 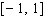 .
.
(Multiple Choice)
4.7/5  (30)
(30)
Showing 21 - 40 of 66
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)