Exam 3: Exponential Functions and Models

The number of cell phone users at time t (in years) is modeled by 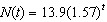. Which one of the following models the number of cell phone users for a one-month growth factor?

Which one of the following scenarios does NOT describe exponential growth?

Using the following table of a function that models exponential decay, determine the one-month decay factor (rounded to the nearest thousandth).

Atmospheric pressure (measured in atm) decreases by 11.5% for every 1000-meter increase in elevation. At sea level, the atmospheric pressure is 1 atm. What is the 8,000-meter decay factor for the atmospheric pressure (rounded to the nearest thousandth)?

Atmospheric pressure (measured in atm) decreases by 11.5% for every 1000-meter increase in elevation. At sea level, the atmospheric pressure is 1 atm. What is the atmospheric pressure at 8,000 meters above sea level (rounded to the nearest thousandth)?

After college graduation, Sheena was offered two different jobs. The first offer included a salary of $40,300 plus a guaranteed raise of $1100 per year. The second offer included a salary of $29,000 plus a guaranteed raise of 3% per year. Use the first job offer to find a function f that models the salary t years from now.

The number of tourists in a small town at time t (in years) is modeled by 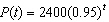. What is the initial number of tourists?

Using the following table of a function that models exponential growth, determine which one of the following models the population as a function of time.

A lake is initially stocked with 500 turtles and the turtle population is sampled at 8-week intervals to estimate the population size. The table illustrates the data gathered from the sampling. Using a graphing calculator, find an appropriate curve that models the turtle population as a function of the number of weeks (round to the nearest thousandth).

Which one of the following functions is described by the graph?

The population of Arizona was 5.1 million in 2000 and 7.7 million in 2008. If the population grew linearly, which one of the following models the population as a function of time (in years since 2000)?

The table represents data for an exponential function.

Using the graph below, find the percentage rate of change from to .

What is the percentage rate of change in f from 3 to 6?

Using the following table of a function that models exponential growth, determine the one-year growth factor (rounded to the nearest thousandth).

The function 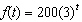is a model for a population A, where t is measured in years. The function 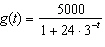is a model for a population B, where t is measured in years. True or false? -The function f(t) grows linearly.

The population of Smallville at time t (in years) is modeled by 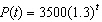. What is the growth rate (in percentage form)?

The amount of caffeine (in milligrams) left in an adult body t hours after drinking a 16 oz. coke is modeled by 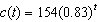. What is the initial population?

The number of bacteria present in a Petri dish at time t (in minutes) is modeled by 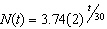. Which one of the following models the population for a one-hour growth factor?

In 1990, a town s population was 24,127. In 1998, the town s population increased to 33,887. Assuming that the population increased exponentially from 1990-1998, this data can be modeled by 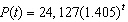where t is the number of years since 1990.