Exam 2: Linear Programming Models: Graphical and Computer Methods

It is possible for a linear programming model to yield an optimal solution that has fractional values.

Consider the following linear programming model This linear programming model has: Min 2+3 Subject to: +\geq4 \geq2 ,\geq0

Figure 1: 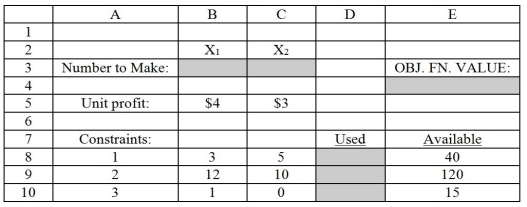Figure 1 demonstrates an Excel spreadsheet that is used to model the following linear programming problem: Max : 4+3 Subject to: 3+5\leq40 12+10\leq120 \geq15 ,\geq0 Note: Cells B3 and C3 are the designated cells for the optimal values of X₁ and X₂,respectively,while cell E4 is the designated cell for the objective function value.Cells D8:D10 designate the left-hand side of the constraints. -Refer to Figure 1.What cell reference designates the Target Cell in "Solver"?

A company that is introducing a new product would like to generate maximum market exposure.The marketing department currently has $100,000 of advertising budget for the year and is considering placing ads in three media: radio,television,and newspapers.The cost per ad and the exposure rating are as follows: Cost/ad Exposure/ad Radio \ 10,000 30,000 individuals Television \ 25,000 50,000 individuals Newspaper \ 5000 20,000 individuals The marketing department would like to place twice as many radio ads as television ads.They also would like to place at least 4 ads in each advertising media.What is the optimal allocation to each advertising medium to maximize audience exposure?

The constraint for a given resource is given by the following equation: 2X₁ + 3X₂ ≥ 20 If X₁ = 5 and X₂ = 4 how many units of this resource are unused?

A company manufactures four products A,B,C,and D that must go through assembly,polishing,and packing before being shipped to a wholesaler.For each product,the time required for these operations is shown below (in minutes)as is the profit per unit sold. The company estimates that each year they have 1667 hours of assembly time,833 hours of polishing time and 1000 hours of packing time available.How many of each product should the company make per year to maximize its yearly profit?

A linear programming model has the following two constraints: X₁ ≥ 3 and X₁ ≥ 4.This model has a redundant constraint.

Suppose that a farmer has 5 acres of land that can be planted with either wheat,corn,or a combination of the two.To ensure a healthy crop,a fertilizer and an insecticide must be applied at the beginning of the season before harvesting.The farmer currently has 100 pounds of the fertilizer and 150 pounds of the insecticide at the beginning of the season.Each acre of wheat planted requires 10 pounds of the fertilizer and 12 pounds of the insecticide.Each acre of corn planted requires 13 pounds of the fertilizer and 11 pounds of the insecticide.Each acre of wheat harvested yields a profit of $600,while each acre of corn harvested yields $750 in profit.What is the optimal allocation for the crops that maximizes the farmer's profit?

Figure 1: Figure 1 demonstrates an Excel spreadsheet that is used to model the following linear programming problem: Max : 4+3 Subject to: 3+5\leq40 12+10\leq120 \geq15 ,\geq0 Note: Cells B3 and C3 are the designated cells for the optimal values of X₁ and X₂,respectively,while cell E4 is the designated cell for the objective function value.Cells D8:D10 designate the left-hand side of the constraints. -Refer to Figure 1.What formula should be entered in cell D9 to compute the amount of resource 2 that is consumed?

The simplex method is an algebraic solution procedure for a linear programming problem.

If a linear programming problem has alternate optimal solutions,then the objective function value will vary according to each alternate optimal point.

In a product mix problem,a decision maker has limited availability of weekly labor hours.Labor hours would most likely constitute a decision variable rather than a constraint.

________ systematically examines corner points,using algebraic steps,until an optimal solution is found.

Consider the following linear programming problem. Maximize 6+4 Subject to: +2\leq16 3+2\leq24 \geq2 ,\geq0 Use Solver to find the optimal values of X₁ and X₂.

A linear programming model generates an optimal solution with fractional values.This solution satisfies which basic linear programming assumption?

A carpenter makes tables and chairs.Each table can be sold for a profit of $50 and each chair for a profit of $30.The carpenter works a maximum of 40 hours per week and spends 5 hours to make a table and 2 hours to make a chair.Customer demand requires that he makes at least twice as many chairs as tables.The carpenter stores the finished products in his garage,and there is room for a maximum of 6 furniture pieces each week.Determine the carpenter's optimal production mix.

Consider the following linear programming model: Max + Subject to: +\leq2 \geq1 \geq3 ,\geq0 This linear programming model has:

Unbounded linear programming problems typically arise as a result of misformulation.

If a redundant constraint is eliminated from a linear programming model,this will have an impact on the optimal solution.

Linear programming models typically do not have coefficients (i.e. ,objective function or constraint coefficients)that assume random values.