A warehouse stocks five different products,A,B,C,and D.The warehouse has a total of 100,000 square feet of floor space available to accommodate all the products that it inventories.The monthly profit per square foot for each product is as follows: \[\begin{array}{l} \underline{\text { Product }} \quad\underline{ \text { Profit per square foot }}\\ \begin{array} { l l } \mathrm { A } && &&\$ 4.50 \\ \mathrm {~B} &&&& \$ 3.00 \\ \mathrm { C } && &&\$ 2.75 \\ \mathrm { D } &&&& \$ 3.75 \end{array} \end{array}\] Each product must have at least 10,000 ft²,and no single product can have more than 25% of the total warehouse space.The warehouse manager wants to know the floor space that should be allocated to each product to maximize profit.

The answer of A warehouse stocks five different products,A,B,C,and D.The...

An ice cream shop sells single scoop ice cream cones that come in three flavors: chocolate only,vanilla only,and chocolate-vanilla twist.The cones are prepackaged and sold to a supermarket daily.The ingredients used along with the minimum demand of each flavor are shown as follows: \[\begin{array}{l} \begin{array} { l l l l } & &\underline{ \text { Ice Cream Flavor }} \\ & \underline{\text { Chocolate } }&\underline{ \text { Vanilla } }& \underline{\text { Chocolate-Vanilla }} \\ \text { Ingredient: } & & & \\ \text { Chocolate } & 4 \mathrm { oz } & 0 \mathrm { oz } . & 3 \mathrm { oz } . \\ \text { Vanilla } & 0 \mathrm { oz } & 4 \mathrm { oz } & 2 \mathrm { oz } . \end{array}\\ \end{array}\] $\text { Min daily demand: } \quad 20 \text { scoops }\quad 15 \text { scoops } \quad \quad \quad \quad 10 \text { scoops }$ Each day,40 pounds of chocolate and 38 pounds of vanilla are supplied to the ice cream shop from an outside vendor.The chocolate,vanilla,and chocolate-vanilla twist each yield a profit of $2.00,$2.50,and $3.00 per cone,respectively.How many chocolate,vanilla,and chocolate-vanilla twist cones must prepackage daily to maximize daily profits?

The answer of An ice cream shop sells single scoop...

Consider the following linear programming model \[\begin{array} { l l } \operatorname { Max } & 2 \mathrm { X } _ { 1 } + 3 \mathrm { X } _ { 2 } \\ \text { Subject to: } & \\ & \mathrm { X } _ { 1 } + \mathrm { X } _ { 2 } \geq 4 \\ & \mathrm { X } _ { 1 } \geq 2 \\ & \mathrm { X } _ { 1 } , \mathrm { X } _ { 2 } \geq 0 \end{array}\] This linear programming model has:

A) redundant constraints B) infeasible solution C) alternate optimal solution D) unique solution E) unbounded solution A) redundant constraints B) infeasible solution C) alternate optimal solution D) unique solution E) unbounded solution

Consider the following linear programming model: \[\begin{array} { l l } \operatorname { Max } & 2 \mathrm { X } _ { 1 } + 3 \mathrm { X } _ { 2 } \\ \text { Subject to: } & \\ & \mathrm { X } _ { 1 } \leq 2 \\ & \mathrm { X } _ { 2 } \leq 3 \\ & \mathrm { X } _ { 1 } \leq 1 \\ & \mathrm { X } _ { 1 } , \mathrm { X } _ { 2 } \geq 0 \end{array}\] This linear programming model has:

A) alternate optimal solutions B) unbounded solution C) redundant constraint D) infeasible solution E) non-negative solution A) alternate optimal solutions B) unbounded solution C) redundant constraint D) infeasible solution E) non-negative solution

Exam 2: Linear Programming Models: Graphical and Computer Methods

A bank is attempting to determine where its assets should be allocated in order to maximize its annual return.At present,$750,000 is available for investment in three types of mutual funds: A,B,and C.The annual rate of return on each type of fund is as follows: fund A,15%;fund B,12%;fund C;13%.The bank's manager has placed the following restrictions on the bank's portfolio: • No more than 20% of the total amount invested may be in fund A. • The amount invested in fund B cannot exceed the amount invested in fund C. Determine the optimal allocation that maximizes the bank's annual return.

(Essay)

4.9/5

(30)

Question 21

A computer retail store sells two types of flat screen monitors: 17 inches and 19 inches,with a profit contribution of $300 and $250,respectively.The monitors are ordered each week from an outside supplier.As an added feature,the retail store installs on each monitor a privacy filter that narrows the viewing angle so that only persons sitting directly in front of the monitor are able to see on-screen data.Each 19" monitor consumes about 30 minutes of installation time,while each 17" monitor requires about 10 minutes of installation time.The retail store has approximately 40 hours of labor time available each week.The total combined demand for both monitors is at least 40 monitors each week.How many units of each monitor should the retail store order each week to maximize its weekly profits and meet its weekly demand?

(Essay)

4.8/5

(35)

Question 22

Figure 1: $Figure 1: 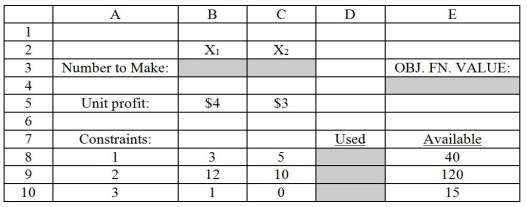Figure 1 demonstrates an Excel spreadsheet that is used to model the following linear programming problem: \begin{array} { l l } \operatorname { Max } : & 4 \mathrm { X } _ { 1 } + 3 \mathrm { X } _ { 2 } \\ \text { Subject to: } & \\ & 3 \mathrm { X } _ { 1 } + 5 \mathrm { X } _ { 2 } \leq 40 \\ & 12 \mathrm { X } _ { 1 } + 10 \mathrm { X } _ { 2 } \leq 120 \\ & \mathrm { X } _ { 1 } \geq 15 \\ & \mathrm { X } _ { 1 } , \mathrm { X } _ { 2 } \geq 0 \end{array} Note: Cells B3 and C3 are the designated cells for the optimal values of X₁ and X₂,respectively,while cell E4 is the designated cell for the objective function value.Cells D8:D10 designate the left-hand side of the constraints. -Refer to Figure 1.What formula should be entered in cell E4 to compute total profitability?$ Figure 1 demonstrates an Excel spreadsheet that is used to model the following linear programming problem: Max : 4+3 Subject to: 3+5\leq40 12+10\leq120 \geq15 ,\geq0 Note: Cells B3 and C3 are the designated cells for the optimal values of X₁ and X₂,respectively,while cell E4 is the designated cell for the objective function value.Cells D8:D10 designate the left-hand side of the constraints. -Refer to Figure 1.What formula should be entered in cell E4 to compute total profitability?

(Multiple Choice)

4.8/5

(33)

Question 23

It is possible to solve graphically a linear programming model with 4 decision variables.

(True/False)

4.9/5

(33)

Question 24

A warehouse stocks five different products,A,B,C,and D.The warehouse has a total of 100,000 square feet of floor space available to accommodate all the products that it inventories.The monthly profit per square foot for each product is as follows: \ 4.50 \ 3.00 \ 2.75 \ 3.75 Each product must have at least 10,000 ft²,and no single product can have more than 25% of the total warehouse space.The warehouse manager wants to know the floor space that should be allocated to each product to maximize profit.

(Essay)

4.8/5

(40)

Question 25

An ice cream shop sells single scoop ice cream cones that come in three flavors: chocolate only,vanilla only,and chocolate-vanilla twist.The cones are prepackaged and sold to a supermarket daily.The ingredients used along with the minimum demand of each flavor are shown as follows: Ingredient: Chocolate 4 0. 3. Vanilla 0 4 2. $\text { Min daily demand: } \quad 20 \text { scoops }\quad 15 \text { scoops } \quad \quad \quad \quad 10 \text { scoops }$ Each day,40 pounds of chocolate and 38 pounds of vanilla are supplied to the ice cream shop from an outside vendor.The chocolate,vanilla,and chocolate-vanilla twist each yield a profit of $2.00,$2.50,and $3.00 per cone,respectively.How many chocolate,vanilla,and chocolate-vanilla twist cones must prepackage daily to maximize daily profits?

(Essay)

4.9/5

(37)

Question 26

If an isoprofit line can be moved outward such that the objective function value can be made to reach infinity,then this problem has an unbounded solution.

(True/False)

4.8/5

(40)

Question 27

Figure 1: $Figure 1: Figure 1 demonstrates an Excel spreadsheet that is used to model the following linear programming problem: \begin{array} { l l } \operatorname { Max } : & 4 \mathrm { X } _ { 1 } + 3 \mathrm { X } _ { 2 } \\ \text { Subject to: } & \\ & 3 \mathrm { X } _ { 1 } + 5 \mathrm { X } _ { 2 } \leq 40 \\ & 12 \mathrm { X } _ { 1 } + 10 \mathrm { X } _ { 2 } \leq 120 \\ & \mathrm { X } _ { 1 } \geq 15 \\ & \mathrm { X } _ { 1 } , \mathrm { X } _ { 2 } \geq 0 \end{array} Note: Cells B3 and C3 are the designated cells for the optimal values of X₁ and X₂,respectively,while cell E4 is the designated cell for the objective function value.Cells D8:D10 designate the left-hand side of the constraints. -Refer to Figure 1.Which cell(s)are the Changing Cells as designated by Solver?$ Figure 1 demonstrates an Excel spreadsheet that is used to model the following linear programming problem: Max : 4+3 Subject to: 3+5\leq40 12+10\leq120 \geq15 ,\geq0 Note: Cells B3 and C3 are the designated cells for the optimal values of X₁ and X₂,respectively,while cell E4 is the designated cell for the objective function value.Cells D8:D10 designate the left-hand side of the constraints. -Refer to Figure 1.Which cell(s)are the Changing Cells as designated by "Solver"?

(Multiple Choice)

4.8/5

(39)

Question 28

When using Solver,the parameter Changing Cells is typically associated with the objective function.

(True/False)

4.8/5

(35)

Question 29

"Solver" typically generates which of the following report(s)?

(Multiple Choice)

4.9/5

(34)

Question 30

A company can decide how many additional labor hours to acquire for a given week.Subcontractors will only work a maximum of 20 hours a week.The company must produce at least 200 units of product A,300 units of product B,and 400 units of product C.In 1 hour of work,worker 1 can produce 15 units of product A,10 units of product B,and 30 units of product C.Worker 2 can produce 5 units of product B,20 units of product B,and 35 units of product C.Worker 3 can produce 20 units of product A,15 units of product B,and 25 units of product C.Worker 1 demands a salary of $50/hr,worker 2 demands a salary of $40/hr,and worker 3 demands a salary of $45/hr.The company must choose how many hours they should hire from each worker to meet their production requirements and minimize labor cost.

(Essay)

4.9/5

(28)

Question 31

The constraint for a given resource is given by the following equation: 2X₁ + 3X₂ ≤ 20 If X₁ = 5 and X₂ = 3,how many units of this resource are unused?

(Multiple Choice)

4.9/5

(30)

Question 32

A linear programming problem has the following two constraints: X₁ ≤ 20 and X₁ ≥ 25.This problem is infeasible.

(True/False)

4.7/5

(31)

Question 33

Karmarkar's method is synonymous with the corner point method.

(True/False)

4.7/5

(34)

Question 34

Consider the following linear programming problem. Maximize 5+3 Subject to: +\leq20 \geq5 \leq10 ,\geq0 Use Solver to find the optimal values of X₁ and X₂.

(Essay)

4.8/5

(28)

Question 35

A linear programming model has the following objective function: Max: X₁² + 3X₂ + 4X₃.This model violates a key linear programming model assumption.

(True/False)

4.9/5

(40)

Question 36

A furniture store produces beds and desks for college students.The production process requires assembly and painting.Each bed requires 6 hours of assembly and 4 hours of painting.Each desk requires 4 hours of assembly and 8 hours of painting.There are 40 hours of assembly time and 45 hours of painting time available each week.Each bed generates $35 of profit and each desk generates $45 of profit.As a result of a labor strike,the furniture store is limited to producing at most 8 beds each week.Determine how many beds and desks should be produced each week to maximize weekly profits.

(Essay)

4.9/5

(31)

Question 37

Consider the following linear programming model Max 2+3 Subject to: +\geq4 \geq2 ,\geq0 This linear programming model has:

(Multiple Choice)

4.9/5

(35)

Question 38

Creatine and protein are common supplements in most bodybuilding products.Bodyworks,a nutrition health store,makes a powder supplement that combines creatine and protein from two ingredients (X₁ and X₂).Ingredient X₁ provides 20 grams of protein and 5 grams of creatine per pound.Ingredient X₂ provides 15 grams of protein and 3 grams of creatine per pound.Ingredients X₁ and X₂ cost Bodyworks $5 and $7 per pound,respectively.Bodyworks wants its supplement to contain at least 30 grams of protein and 10 grams of creatine per pound and be produced at the least cost. Determine what combination will maximize profits.

(Essay)

4.9/5

(35)

Question 39

Consider the following linear programming model: Max 2+3 Subject to: \leq2 \leq3 \leq1 ,\geq0 This linear programming model has:

(Multiple Choice)

4.8/5

(36)

Question 40

Showing 21 - 40 of 48

It is possible to solve graphically a linear programming model with 4 decision variables.

If an isoprofit line can be moved outward such that the objective function value can be made to reach infinity,then this problem has an unbounded solution.

When using Solver,the parameter Changing Cells is typically associated with the objective function.

"Solver" typically generates which of the following report(s)?

The constraint for a given resource is given by the following equation: 2X₁ + 3X₂ ≤ 20 If X₁ = 5 and X₂ = 3,how many units of this resource are unused?

A linear programming problem has the following two constraints: X₁ ≤ 20 and X₁ ≥ 25.This problem is infeasible.

Karmarkar's method is synonymous with the corner point method.

Consider the following linear programming problem. Maximize 5+3 Subject to: +\leq20 \geq5 \leq10 ,\geq0 Use Solver to find the optimal values of X₁ and X₂.

A linear programming model has the following objective function: Max: X₁² + 3X₂ + 4X₃.This model violates a key linear programming model assumption.

Consider the following linear programming model Max 2+3 Subject to: +\geq4 \geq2 ,\geq0 This linear programming model has:

Consider the following linear programming model: Max 2+3 Subject to: \leq2 \leq3 \leq1 ,\geq0 This linear programming model has:

Introduction to Managerial Decision Making

Linear Programming Modeling Applications with Computer Analyses in Excel

Linear Programming Sensitivity Analysis

Transportation, Assignment, and Network Models

Integer, Goal, and Nonlinear Programming Models

Project Management

Decision Analysis

Queuing Models

Simulation Modeling

Forecasting Models

Inventory Control Models

Filters