Exam 4: Linear Programming Sensitivity Analysis

Use this information to answer the following questions. An insurance company has three secretaries,A,B,and C that each is capable of processing four different types of insurance claims.The amount of time required by each secretary to process a particular type of a claim is summarized in the following table. On a typical week,the insurance firm has 5 type 1 claims,4 type 2 claims,2 type 3 claims,and 3 type 4 claims.Each secretary works a maximum of 40 hours per week.The office manager wants to know how many of each type of an insurance claim should be processed by each secretary to minimize the total processing time. Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease SC \1 3 A1 5 0 2 1 1+30 SD \1 3 A2 0 1 3 1+30 1 SE \1 3 A3 0 1 2 1+30 1 SF \1 3 A4 0 3 4 1+30 3 SC \1 4 B1 0 2 4 1+30 2 SD \1 4 B2 0 3 5 1+30 3 SE \1 4 B3 0 2 3 1+30 2 SF \1 4 B4 3 0 1 3 1+30 SC \1 5 C1 0 1 3 1+30 1 SD \1 5 C2 4 0 2 1 1+30 SE \1 5 C3 2 0 1 1 1+30 SF \1 5 C4 0 4 5 1+30 4 Constraints Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \G \1 3 A constraint 10 0 40 1+30 30 \G \1 4 B constraint 3 0 40 1+30 37 \G \1 5 C constraint 10 0 40 1+30 30 \C \1 6 Claim Type 1 5 2 5 15 5 \D \1 6 Claim Type 2 4 2 4 15 4 \E \1 6 Claim Type 3 2 1 2 30 2 \F \1 6 Claim Type 4 3 1 3 37 3 -Use the Sensitivity Report to answer the following questions: a.Which constraints are binding? b.Suppose that secretary A has a total of 45 weekly hours.What impact would this have on the current optimal solution? c.What is the total number of unused weekly hours for secretary B? d.Suppose that the number of type 4 claims increases to 4? What impact would this have on the current optimal solution?

Use this information to answer the following questions. An insurance company has three secretaries,A,B,and C that each is capable of processing four different types of insurance claims.The amount of time required by each secretary to process a particular type of a claim is summarized in the following table. On a typical week,the insurance firm has 5 type 1 claims,4 type 2 claims,2 type 3 claims,and 3 type 4 claims.Each secretary works a maximum of 40 hours per week.The office manager wants to know how many of each type of an insurance claim should be processed by each secretary to minimize the total processing time. Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease SC \1 3 A1 5 0 2 1 1+30 SD \1 3 A2 0 1 3 1+30 1 SE \1 3 A3 0 1 2 1+30 1 SF \1 3 A4 0 3 4 1+30 3 SC \1 4 B1 0 2 4 1+30 2 SD \1 4 B2 0 3 5 1+30 3 SE \1 4 B3 0 2 3 1+30 2 SF \1 4 B4 3 0 1 3 1+30 SC \1 5 C1 0 1 3 1+30 1 SD \1 5 C2 4 0 2 1 1+30 SE \1 5 C3 2 0 1 1 1+30 SF \1 5 C4 0 4 5 1+30 4 Constraints Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \G \1 3 A constraint 10 0 40 1+30 30 \G \1 4 B constraint 3 0 40 1+30 37 \G \1 5 C constraint 10 0 40 1+30 30 \C \1 6 Claim Type 1 5 2 5 15 5 \D \1 6 Claim Type 2 4 2 4 15 4 \E \1 6 Claim Type 3 2 1 2 30 2 \F \1 6 Claim Type 4 3 1 3 37 3 -Use the Sensitivity Report to answer the following questions: a.What is the total minimal processing time in hours? b.Suppose that secretary A can process a type 2 claim in two hours rather than three hours.How would this impact the current optimal solution? c.Assume that secretary C can process a type 4 claim in 6 hours rather than 5 hours.How would this impact the current optimal solution? d.Currently,secretary C is not processing any type 4 claims.Suppose that we force secretary four to process one type 4 claim.What impact would this have on the optimal solution?

Use this information to answer the following questions. An investment company currently has $1 million available for investment in five different stocks.The company wants to maximize the interest earned over the next year.The five investment possibilities along with the expected interest earned are shown below.To manage risk,the investment firm wishes to have at least 35% of the investment in stocks A and B.Furthermore,no more than 15% of the investment may be in stock E. Investment Expected Interest Earned (\%) Stock A 7 Stock B 9 Stock C 8 Stock D 10 Stock E 11 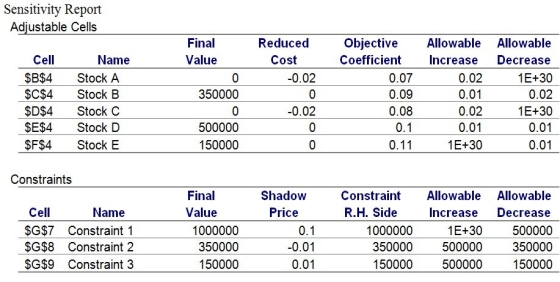-Use the Sensitivity Report to answer the following questions: a.What would be the impact on the optimal allocation if the expected interest earned on stock A decreases to 6%? b.What would be the impact on the optimal allocation if the expected interest earned on stock A increases to 10%? c.What should the minimal expected interest earned for stock C be before it would be desirable to invest in this particular stock? d.What would be the impact on the optimal allocation and the objective function value if the expected interest earned on stock B decreases by 1%?

The slack of a constraint indicates the amount of a used resource.

Use this information,along with its associated Sensitivity Report,to answer the following questions. A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table. Labor (hours) Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week. Formulation \ Max 10+10+10 Subject to: 3++5\leq300 (constraint \#1) 2+4\leq400 (constraint \#2) 4+2+3.5\leq200 (constraint \#3) \geq10 (constraint \#4) ,,\geq0 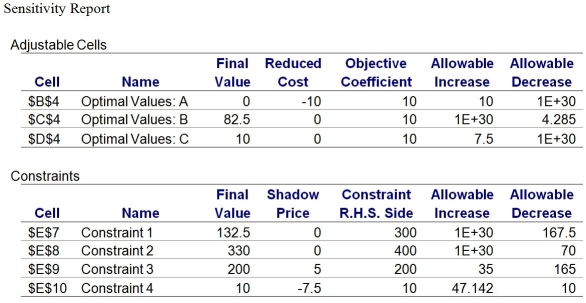-Suppose that the production manager has an additional 100 pounds of material 1.What impact will this have on the current optimal objective function value?

Surplus is typically associated with "≤" constraints.

Use this information,along with its associated Sensitivity Report,to answer the following questions. A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table. Labor (hours) Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week. Formulation \ Max 10+10+10 Subject to: 3++5\leq300 (constraint \#1) 2+4\leq400 (constraint \#2) 4+2+3.5\leq200 (constraint \#3) \geq10 (constraint \#4) ,,\geq0 -Suppose that the production manager procures an additional 10 labor hours.What impact will this have on the current optimal objective function value?

Use the information below to answer the following questions. A real estate developer is planning to build an office complex.Currently,there are three office sizes under consideration: small,medium,and large.Small offices can be rented for $600 per month,medium offices can be rented for $750 per month,and large offices can be rented for $1000 per month.Each small office requires 600 square feet,each medium office requires 800 square feet,and each large office requires 1000 square feet.The current plot of land available to the developer is 100,000 square feet.The developer wants to ensure that the office complex has at least 3 units of each office size.Moreover,zoning restrictions limit the total number of offices to 50. 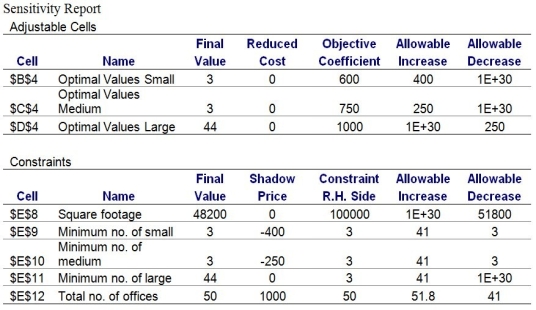-Use the Sensitivity Report to answer the following questions: a.Suppose that the square footage available to the developer increases to 110,000 square feet.What impact would this have on the optimal objective function value? b.Suppose that the minimal number of small officers that the developer needs to build must be at least 5 offices.What impact would this have on the optimal objective function value? c.Suppose that the monthly rental of small offices increases to $650,and that the monthly rental of medium offices increases to $800.What impact will this have on the current optimal solution and the objective function value? d.Suppose that the total number of offices increases to a maximum of 55,and the minimum number of medium offices increases to 5.What impact would this have on the current optimal objective function value?

In pricing out a new variable,the worth or value of resources consumed is typically measured by:

The Reduced Cost may be viewed as the difference between the marginal contribution of a variable and the marginal value of the resources it consumes.

Sensitivity analysis is analogous to postoptimality analysis

Use the information below to answer the following questions. A real estate developer is planning to build an office complex.Currently,there are three office sizes under consideration: small,medium,and large.Small offices can be rented for $600 per month,medium offices can be rented for $750 per month,and large offices can be rented for $1000 per month.Each small office requires 600 square feet,each medium office requires 800 square feet,and each large office requires 1000 square feet.The current plot of land available to the developer is 100,000 square feet.The developer wants to ensure that the office complex has at least 3 units of each office size.Moreover,zoning restrictions limit the total number of offices to 50. -Use the Sensitivity Report to answer the following questions: a.How many small,medium,and large offices should the developer build? b.What is the total optimal monthly revenue? c.Which constraints are binding? Which constraints are non-binding? d.How much square footage would remain unused if the developer implements the optimal solution?

A binding constraint means that the constraint is exactly satisfied,and its left-hand side does not equal its right-hand side.

Use this information to answer the following questions. An investment company currently has $1 million available for investment in five different stocks.The company wants to maximize the interest earned over the next year.The five investment possibilities along with the expected interest earned are shown below.To manage risk,the investment firm wishes to have at least 35% of the investment in stocks A and B.Furthermore,no more than 15% of the investment may be in stock E. Investment Expected Interest Earned (\%) Stock A 7 Stock B 9 Stock C 8 Stock D 10 Stock E 11 -Use the Sensitivity Report to answer the following questions: a.What is the optimal total expected interest earned for next year? b.What is the dollar amount that should be invested in each stock? c.Which constraints are binding? Which constraints are not binding? d.Is the solution to the problem unique or are there alternate optimal solutions? e.Does the optimal solution call for investing the entire $1,000,000?

________ can be used to check whether simultaneous changes in RHS or OFC values can be analyzed by using the current sensitivity report.

Use the information below to answer the following questions. A real estate developer is planning to build an office complex.Currently,there are three office sizes under consideration: small,medium,and large.Small offices can be rented for $600 per month,medium offices can be rented for $750 per month,and large offices can be rented for $1000 per month.Each small office requires 600 square feet,each medium office requires 800 square feet,and each large office requires 1000 square feet.The current plot of land available to the developer is 100,000 square feet.The developer wants to ensure that the office complex has at least 3 units of each office size.Moreover,zoning restrictions limit the total number of offices to 50. -Use the Sensitivity Report to answer the following questions: a.What would be the impact on the optimal allocation of offices and the objective function value if small offices can be rented for $800 per month rather than $600 per month? b.What would be the impact on the optimal allocation of offices and the objective function value if medium offices can be rented for $650 per month rather than $750 per month? c.What would be the impact on the optimal allocation of offices if medium offices can be rented for $1100.00 rather than $750 per month? d.Is the solution to the problem unique or are there alternate optimal solutions?

Use this information to answer the following questions. An investment company currently has $1 million available for investment in five different stocks.The company wants to maximize the interest earned over the next year.The five investment possibilities along with the expected interest earned are shown below.To manage risk,the investment firm wishes to have at least 35% of the investment in stocks A and B.Furthermore,no more than 15% of the investment may be in stock E. Investment Expected Interest Earned (\%) Stock A 7 Stock B 9 Stock C 8 Stock D 10 Stock E 11 -Use the Sensitivity Report to answer the following questions: a.Suppose that the amount of money available for investment increases by $50,000.What impact would this have on the current optimal objective function value? b.Suppose that total investment in stocks A and B must be at least 40% of the total amount available for investment (i.e. ,$400,000).What impact would this have on the current optimal objective function value? c.Suppose that the total investment in stocks A and be must be at least 30% of the total amount available for investment.What impact would this have on the current optimal objective function value? d.Assume that no more than 30% of the investment may be in stock E.What impact would this have on the current optimal objective function value?

Use this information to answer the following questions. An insurance company has three secretaries,A,B,and C that each is capable of processing four different types of insurance claims.The amount of time required by each secretary to process a particular type of a claim is summarized in the following table. On a typical week,the insurance firm has 5 type 1 claims,4 type 2 claims,2 type 3 claims,and 3 type 4 claims.Each secretary works a maximum of 40 hours per week.The office manager wants to know how many of each type of an insurance claim should be processed by each secretary to minimize the total processing time. Cell Name Final Value Reduced Cost Objective Coefficient Allowable Increase Allowable Decrease SC \1 3 A1 5 0 2 1 1+30 SD \1 3 A2 0 1 3 1+30 1 SE \1 3 A3 0 1 2 1+30 1 SF \1 3 A4 0 3 4 1+30 3 SC \1 4 B1 0 2 4 1+30 2 SD \1 4 B2 0 3 5 1+30 3 SE \1 4 B3 0 2 3 1+30 2 SF \1 4 B4 3 0 1 3 1+30 SC \1 5 C1 0 1 3 1+30 1 SD \1 5 C2 4 0 2 1 1+30 SE \1 5 C3 2 0 1 1 1+30 SF \1 5 C4 0 4 5 1+30 4 Constraints Cell Name Final Value Shadow Price Constraint R.H. Side Allowable Increase Allowable Decrease \G \1 3 A constraint 10 0 40 1+30 30 \G \1 4 B constraint 3 0 40 1+30 37 \G \1 5 C constraint 10 0 40 1+30 30 \C \1 6 Claim Type 1 5 2 5 15 5 \D \1 6 Claim Type 2 4 2 4 15 4 \E \1 6 Claim Type 3 2 1 2 30 2 \F \1 6 Claim Type 4 3 1 3 37 3 -Use the Sensitivity Report to answer the following questions: a.Suppose that the number of type 1 claims increases to 6 and the number of type 2 claims decreases to 3.What impact would this simultaneous change have on the current optimal objective function value? b.What is the impact on the current solution and the objective function value if secretary A takes 3 hours to process claim 1 and secretary B takes 5 hours to process claim 1?

Use this information,along with its associated Sensitivity Report,to answer the following questions. A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table. Labor (hours) Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week. Formulation \ Max 10+10+10 Subject to: 3++5\leq300 (constraint \#1) 2+4\leq400 (constraint \#2) 4+2+3.5\leq200 (constraint \#3) \geq10 (constraint \#4) ,,\geq0 -What is the optimal objective function value?

When the Allowable Increase or Allowable Decrease columns for the objective function coefficient of a variable has a value of zero in the Adjustable Cells table,this indicates the presence of a unique solution.