Exam 4: Linear Programming Sensitivity Analysis
Exam 1: Introduction to Managerial Decision Making41 Questions
Exam 2: Linear Programming Models: Graphical and Computer Methods48 Questions
Exam 3: Linear Programming Modeling Applications with Computer Analyses in Excel49 Questions
Exam 4: Linear Programming Sensitivity Analysis44 Questions
Exam 5: Transportation, Assignment, and Network Models37 Questions
Exam 6: Integer, Goal, and Nonlinear Programming Models55 Questions
Exam 7: Project Management52 Questions
Exam 8: Decision Analysis53 Questions
Exam 9: Queuing Models47 Questions
Exam 10: Simulation Modeling54 Questions
Exam 11: Forecasting Models64 Questions
Exam 12: Inventory Control Models39 Questions
Select questions type
Impact of changes in RHS values of constraints is typically measured by the:
(Multiple Choice)
4.8/5  (24)
(24)
A company can decide how many additional labor hours to acquire for a given week.Subcontractors will only work a maximum of 20 hours a week.The company must produce at least 200 units of product A,300 units of product B,and 400 units of product C.In 1 hour of work,worker 1 can produce 15 units of product A,10 units of product B,and 30 units of product C.Worker 2 can produce 5 units of product B,20 units of product B,and 35 units of product C.Worker 3 can produce 20 units of product A,15 units of product B,and 25 units of product C.Worker 1 demands a salary of $50/hr,worker 2 demands a salary of $40/hr,and worker 3 demands a salary of $45/hr.The company must choose how many hours they should hire from each worker to meet their production requirements and minimize labor cost.The sensitivity report is displayed below.
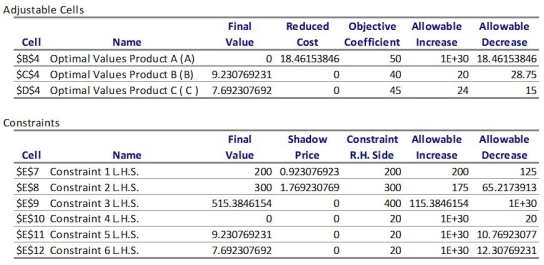 Answer the following questions:
a.How much of products A,B,and C should be produced?
b.Which constraints are binding? Which constraints are non-binding?
c.If constraint 2 is relaxed by one unit,how will the objective value be affected?
Answer the following questions:
a.How much of products A,B,and C should be produced?
b.Which constraints are binding? Which constraints are non-binding?
c.If constraint 2 is relaxed by one unit,how will the objective value be affected?
(Essay)
4.9/5  (41)
(41)
Assume that the shadow price of a non-binding "≤" constraint is 5.This implies that:
(Multiple Choice)
4.9/5  (33)
(33)
The 100% Rule can be using to measure simultaneous changes in which of the following?
(Multiple Choice)
4.8/5  (38)
(38)
Use this information,along with its associated Sensitivity Report,to answer the following questions.
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.
Labor (hours)
Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week.
Formulation \ Max 10+10+10 Subject to: 3++5\leq300 (constraint \#1) 2+4\leq400 (constraint \#2) 4+2+3.5\leq200 (constraint \#3) \geq10 (constraint \#4) ,,\geq0
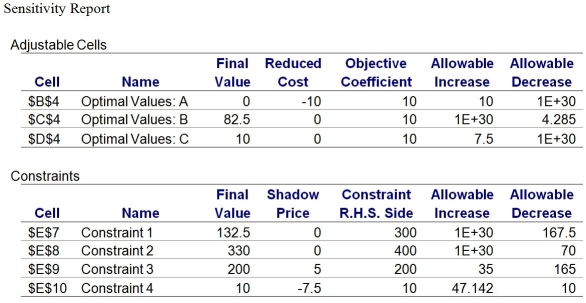 -Suppose that the objective function coefficient for product C increases by $8.What impact will this have on the current values of the optimal solution?
-Suppose that the objective function coefficient for product C increases by $8.What impact will this have on the current values of the optimal solution?
(Multiple Choice)
4.8/5  (37)
(37)
The information provided in the Sensitivity Report assumes that we are considering a change to only a single input data value.
(True/False)
4.8/5  (35)
(35)
As long as the objective function coefficient for a given variable increases within its allowable increase,the current optimal solution remains the same
(True/False)
4.9/5  (39)
(39)
Optimal solutions to linear programming problems are found under probabilistic assumptions.
(True/False)
4.8/5  (30)
(30)
The presence of zeros in the Allowable Increase or Allowable decrease columns for objective function values indicates:
(Multiple Choice)
4.8/5  (32)
(32)
The slack values in the Answer Report can refer to either slack or surplus values based on the type of the inequality.
(True/False)
4.8/5  (27)
(27)
A constraint right-hand side value is increased within its allowable increase value.The shadow price for this constraint will still be valid.
(True/False)
4.9/5  (37)
(37)
The Sensitivity Report has two parts: one part deals with objective function coefficient changes,and the other part deals with constraint coefficient changes.
(True/False)
4.8/5  (35)
(35)
Use this information to answer the following questions.
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:
Demand (units) Capacity (units) R1:300 F1:250 R2: 500 F2: 350 R3:200 F3:400
The company wants to come up with an optimal shipping strategy that will allow it to minimize its total shipping cost.
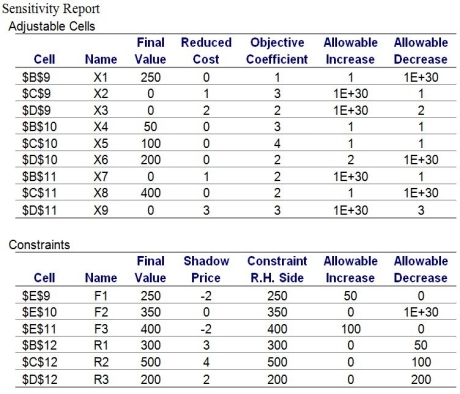 -Use the Sensitivity Report to answer the following questions:
a.Suppose that the shipping cost per unit for variable X1 (i.e. ,route F1-R1)increases to $2.00.What impact will this have on the current optimal solution and the objective function value?
b.Suppose that the shipping cost per unit for variable X6 (i.e. ,route F2-R3)increases by $2.00 to $5.00.What impact will this have on the current optimal solution and the objective function value?
c.Suppose that the factory constraints and the retail outlet constraints become "≤".What would the optimal solution and the objective function coefficient be? (Hint: The answer to this question is not given in the Sensitivity Report. )
-Use the Sensitivity Report to answer the following questions:
a.Suppose that the shipping cost per unit for variable X1 (i.e. ,route F1-R1)increases to $2.00.What impact will this have on the current optimal solution and the objective function value?
b.Suppose that the shipping cost per unit for variable X6 (i.e. ,route F2-R3)increases by $2.00 to $5.00.What impact will this have on the current optimal solution and the objective function value?
c.Suppose that the factory constraints and the retail outlet constraints become "≤".What would the optimal solution and the objective function coefficient be? (Hint: The answer to this question is not given in the Sensitivity Report. )
(Essay)
4.9/5  (40)
(40)
A given constraint has 40 unused hours.The shadow price for this resource would most likely be zero.
(True/False)
4.9/5  (36)
(36)
Use this information,along with its associated Sensitivity Report,to answer the following questions.
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.
Labor (hours)
Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week.
Formulation \ Max 10+10+10 Subject to: 3++5\leq300 (constraint \#1) 2+4\leq400 (constraint \#2) 4+2+3.5\leq200 (constraint \#3) \geq10 (constraint \#4) ,,\geq0
 -Which constraints are binding?
-Which constraints are binding?
(Multiple Choice)
4.9/5  (30)
(30)
Use this information,along with its associated Sensitivity Report,to answer the following questions.
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.
Labor (hours)
Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week.
Formulation \ Max 10+10+10 Subject to: 3++5\leq300 (constraint \#1) 2+4\leq400 (constraint \#2) 4+2+3.5\leq200 (constraint \#3) \geq10 (constraint \#4) ,,\geq0
 -By how much would the profit contribution of product A has to increase before it will be profitable to produce A?
-By how much would the profit contribution of product A has to increase before it will be profitable to produce A?
(Multiple Choice)
4.8/5  (27)
(27)
Use this information to answer the following questions.
A company can ship its product from any of its three factories,F1,F2,and F3,to any of its retail outlets,R1,R2,and R3.The capacity,demand,and shipping cost information is provided as follows:
Demand (units) Capacity (units) R1:300 F1:250 R2: 500 F2: 350 R3:200 F3:400
The company wants to come up with an optimal shipping strategy that will allow it to minimize its total shipping cost.
 -Use the Sensitivity Report to answer the following questions:
a.Will any of the retail outlets experience any shortages in meeting their demand requirements if we implement the optimal solution?
b.Will any of the factories have any remaining quantities of the product if we implement the optimal solution?
c.What is the total minimal shipping cost?
-Use the Sensitivity Report to answer the following questions:
a.Will any of the retail outlets experience any shortages in meeting their demand requirements if we implement the optimal solution?
b.Will any of the factories have any remaining quantities of the product if we implement the optimal solution?
c.What is the total minimal shipping cost?
(Essay)
4.9/5  (27)
(27)
A change in the right-hand side value of a binding constraint usually affects the size of the feasible region.
(True/False)
4.8/5  (31)
(31)
Showing 21 - 40 of 44
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)