Question 1

Surplus is typically associated with which type of constraints?

Accepted Answer

A) ≤ 
B) ≥ 
C) = 
D) ≠ 
E) ± 
A) ≤ 
B) ≥ 
C) = 
D) ≠ 
E) ±

Question 2

The Sensitivity Report typically analyses the impact of simultaneous changes in the objective function coefficients and right-hand side constraint values on the optimal solution.

Accepted Answer

A) True 
 B)False

Question 3

Assume that the reduced cost of a decision variable is -$20 for a maximization problem.This implies that:

Accepted Answer

A) the objective function value will decrease by $20 if we do not produce any units of this product 
B) the objective function value will not change if we produce an additional unit of this product 
C) the objective function value will increase by $20 if we produce an additional unit of this product 
D) the shadow price value will decrease by $20 if we produce an additional unit of this product 
E) the objective function value will decrease by $20 if we produce an additional unit of this product 
A) the objective function value will decrease by $20 if we do not produce any units of this product 
B) the objective function value will not change if we produce an additional unit of this product 
C) the objective function value will increase by $20 if we produce an additional unit of this product 
D) the shadow price value will decrease by $20 if we produce an additional unit of this product 
E) the objective function value will decrease by $20 if we produce an additional unit of this product

Question 4

Use this information,along with its associated Sensitivity Report,to answer the following questions.
A production manager wants to determine how many units of each product to produce weekly to maximize weekly profits.Production requirements for the products are shown in the following table.
 $$\begin{array} { | c | c | c | c | } 
\hline \underline { \text { Product } } & \frac { \text { Material 1 } } { ( \mathrm { lbs } ) } & \frac { \text { Material 2 } } { ( \mathrm { lbs } . ) } & \text { Labor (hours) } \
\hline \underline { \underline { \mathrm { A } } } & \underline { 3 } & \underline { 2 } & \underline { 4 } \
\hline \underline { \mathrm { B } } & \underline { 1 } & \underline { 4 } & \underline { 2 } \
\hline \underline { \mathrm { C } } & \underline { 5 } & \underline { \text { none } } & \underline { 3.5 } \
\hline
\end{array}$$ 
Material 1 costs $7 a pound,material 2 costs $5 a pound,and labor costs $15 per hour.Product A sells for $101 a unit,product B sells for $67 a unit,and product C sells for $97.50 a unit.Each week there are 300 pounds of material 1;400 pounds of material 2;and 200 hours of labor.The output of product A should not be more than one-half of the total number of units produced.Moreover,there is a standing order of 10 units of product C each week.
 $$\begin{array}{l}
\text { Formulation }\
\begin{array} { l l } 
\ { \text { Max } } & 10 \mathrm {~A} + 10 \mathrm {~B} + 10 \mathrm { C } \
\text { Subject to: } & \
& 3 \mathrm {~A} + \mathrm { B } + 5 \mathrm { C } \leq 300 \text { (constraint \#1) } \
& 2 \mathrm {~A} + 4 \mathrm {~B} \leq 400 \text { (constraint \#2) } \
& 4 \mathrm {~A} + 2 \mathrm {~B} + 3.5 \mathrm { C } \leq 200 \text { (constraint \#3) } \
& \mathrm { C } \geq 10 \text { (constraint \#4) } \
& \mathrm { A } , \mathrm { B } , \mathrm { C } \geq 0
\end{array}
\end{array}$$ 
  
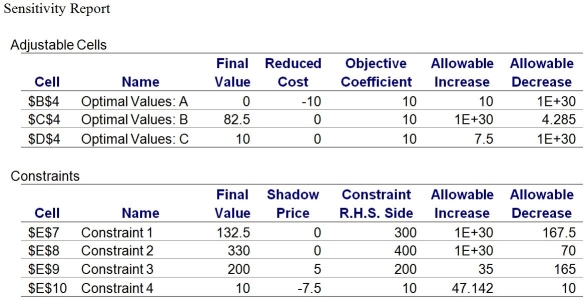-Suppose that we force the production of one unit of product A.The new objective function value will be

Accepted Answer

A) $925 
B) $915 
C) $935 
D) $900 
E) Not enough information is provided. 
A) $925 
B) $915 
C) $935 
D) $900 
E) Not enough information is provided.

Surplus is typically associated with which type of constraints?

The Sensitivity Report typically analyses the impact of simultaneous changes in the objective function coefficients and right-hand side constraint values on the optimal solution.

Assume that the reduced cost of a decision variable is -$20 for a maximization problem.This implies that:

Introduction to Managerial Decision Making

Linear Programming Models: Graphical and Computer Methods

Linear Programming Modeling Applications with Computer Analyses in Excel

Transportation, Assignment, and Network Models

Integer, Goal, and Nonlinear Programming Models

Project Management

Decision Analysis

Queuing Models

Simulation Modeling

Forecasting Models

Inventory Control Models

Filters

Exam 4: Linear Programming Sensitivity Analysis

Surplus is typically associated with which type of constraints?

The Sensitivity Report typically analyses the impact of simultaneous changes in the objective function coefficients and right-hand side constraint values on the optimal solution.

Assume that the reduced cost of a decision variable is -$20 for a maximization problem.This implies that:

Introduction to Managerial Decision Making

Linear Programming Models: Graphical and Computer Methods

Linear Programming Modeling Applications with Computer Analyses in Excel

Transportation, Assignment, and Network Models

Integer, Goal, and Nonlinear Programming Models

Project Management

Decision Analysis

Queuing Models

Simulation Modeling

Forecasting Models

Inventory Control Models

Filters