Question 1

All of the following are possible effects of multicollinearity except

Accepted Answer

A)  the standard error of the regression coefficients may be larger than expected. 
B)  the signs of the regression coefficients may be opposite of what is expected. 
C)  regression coefficients can be quite unstable across samples. 
D)  R2 may be significant, yet none of the predictors are significant. 
E)  the VIF is 0 for all predictors. 
A)  the standard error of the regression coefficients may be larger than expected. 
B)  the signs of the regression coefficients may be opposite of what is expected. 
C)  regression coefficients can be quite unstable across samples. 
D)  R2 may be significant, yet none of the predictors are significant. 
E)  the VIF is 0 for all predictors. E

Question 2

Calculate the partial correlation r12.3 and the part correlation r1(2.3) from the following bivariate correlations: r12 = .3, r13 = -.5, r23 = -.8.

Accepted Answer

Because r₁₂ = .3, r₁₃ = -.5, and r₂₃ = -.8.

\begin{array}{l}r_{12.3}=\frac{r_{12}-r_{18} r_{28}}{\sqrt{\left(1-r_{18}^{2}\right)\left(1-r_{23}^{2}\right)}}=\frac{.3-(-.5)(-.8)}{\sqrt{(.75)(.36)}}=-.1925 \\r_{1(2.3)}=\frac{r_{12}-r_{18} r_{28}}{\sqrt{\left(1-r_{28}^{2}\right)}}=\frac{.3-(-.5)(-.8)}{\sqrt{\left(1-.8^{2}\right)}}=\frac{-.1}{\sqrt{.36}}=-.1667 .\end{array}

Question 3

Carol is building a multiple regression model to predict college GPA from a set of predictors. There is theory suggesting that college GPA can be predicted by students' involvement in college when controlling for their prior achievement. Therefore, Carol first entered into the model a set of variables that measure prior achievement (e.g., high school GPA, SAT), and then added a set of variables that measure collegial involvement. Which one of the following procedures is used?

Accepted Answer

A)  Backward elimination 
B)  Forward selection 
C)  Stepwise selection 
D)  Hierarchical regression 
A)  Backward elimination 
B)  Forward selection 
C)  Stepwise selection 
D)  Hierarchical regression C

Question 4

The correlation between temperature (X1) and the consumption of ice cream (X2) controlling for price of ice cream (X3) can be denoted by

Accepted Answer

A)  r2.13 
B)  r12.3 
C)  r13.2 
D)  r1(2.3) 
E)  r2(1.3) 
A)  r2.13 
B)  r12.3 
C)  r13.2 
D)  r1(2.3) 
E)  r2(1.3)

Question 5

A researcher would like to predict GPA from a set of three predictor variables for a sample of 34 college students. Multiple linear regression analysis was utilized. Complete the following summary table ($\alpha$= .05) for the test of significance of the overall regression model:
 $\begin{array}{lllllll}
\hline \text { Source } & S S & d f & M S & F & \text { Critical Value } & \text { Decision } \
\hline \begin{array}{c}
\text { Regression } \
\text { Residual } \
\text { Total }
\end{array} & & & 6.5 & & & \
\hline
\end{array}$

Accepted Answer

There are three independent variables, s

Question 6

The correlation of GPA (X1) and the number of hours spent on watching TV (X2) where the influence of IQ (X3) is removed from GPA only can be denoted by

Accepted Answer

A)  r2.13 
B)  r12.3 
C)  r13.2 
D)  r1(2.3) 
E)  r2(1.3) 
A)  r2.13 
B)  r12.3 
C)  r13.2 
D)  r1(2.3) 
E)  r2(1.3)

Question 7

You are given the following data, where X1 (attendance rate) and X2 (average SAT score) are to be used to predict Y (average score in graduation test). Each case represents one school.
 $\begin{array}{|c|c|c|}
\hline Y & X_{\mathbf{1}} & X_{\mathbf{2}} \
\hline 78.4 & 93.4 & 1010 \
\hline 81.3 & 94.6 & 1020 \
\hline 81.3 & 95.4 & 1024 \
\hline 82.5 & 91.1 & 1136 \
\hline 77.8 & 91.6 & 952 \
\hline 84.5 & 94.2 & 1042 \
\hline 88.2 & 94.5 & 1106 \
\hline 88.7 & 93.4 & 1004 \
\hline 72.5 & 92.1 & 880 \
\hline 85.4 & 94.9 & 1124 \
\hline 82.9 & 94.3 & 1124 \
\hline 81.4 & 94.7 & 996 \
\hline
\end{array}$ Determine the following values: intercept, b1, b2, SSres, SSreg, F, sres2, s(b1), s(b2), t1, t2.

Accepted Answer

Intercept = -36.536, b₁ = .86

Question 8

In a multiple regression model, Y is predicted from X1, X2, and X3. Both R2 and Radj2 are computed. If X3 is removed from the model, how will R2 change?

Accepted Answer

A)  R2 will increase. 
B)  R2 will decrease. 
C)  R2 will not change. 
D)  uncertain. 
A)  R2 will increase. 
B)  R2 will decrease. 
C)  R2 will not change. 
D)  uncertain.

Question 9

David is studying the correlation of temperature (X1) and the consumption of ice cream (X2). As he expects that the price of ice cream (X3) is correlated with both temperature and the consumption of ice cream, he would like to remove the effects of price from both X1 and X2 when computing the correlation. This is an example of which one of the following?

Accepted Answer

A)  Bivariate correlation 
B)  Partial correlation 
C)  Semipartial correlation 
D)  Regression correlation 
A)  Bivariate correlation 
B)  Partial correlation 
C)  Semipartial correlation 
D)  Regression correlation

Question 10

Karen wants to use a categorical variable, levels of education, to predict annual income. There are six categories in the levels of education: High school graduate, Some college, Associate's degree, Bachelor's degree, Master's degree, Doctorate, or professional degree. How many categories need to be dummy coded and included in the regression model as predictors?

Accepted Answer

A)  4 
B)  5 
C)  6 
D)  7 
A)  4 
B)  5 
C)  6 
D)  7

Question 11

Carol is studying the correlation of college GPA (X1) and the number of hours spent on watching TV (X2). As intelligence is expected to affect GPA, she would like to remove the influence of IQ (X3) from GPA scores when computing the correlation. This is an example of which one of the following?

Accepted Answer

A)  Bivariate correlation 
B)  Partial correlation 
C)  Semipartial correlation 
D)  Regression correlation 
A)  Bivariate correlation 
B)  Partial correlation 
C)  Semipartial correlation 
D)  Regression correlation

Question 12

An instructor wanted to know if the scores on pop quizzes are good predictors of the scores on the final exam. He used the following regression model,
Yi = b1X1i + b2X2i + b3X3i + a + ei, where Y is the score on the final exam, X1 is the score on the first quiz, X2 is the score on the second quiz, and X3 is the average score of the two quizzes. Evaluate this model.

Accepted Answer

A)  The assumption of independence is violated. 
B)  The assumption of linearity is violated. 
C)  The assumption of noncollinearity is violated. 
D)  There is no indication of assumption violation based on the information given. 
A)  The assumption of independence is violated. 
B)  The assumption of linearity is violated. 
C)  The assumption of noncollinearity is violated. 
D)  There is no indication of assumption violation based on the information given.

Question 13

Suppose for the three variables, GPA (X1), time spent on watching TV (X2), and IQ (X3), the bivariate correlation coefficients are computed as below:
R12 = -0.4; r13 = 0.6; r23 = 0.
If we remove the influence of IQ from GPA, the correlation of GPA and the time spent on watching TV will be

Accepted Answer

A)  stronger than the bivariate correlation r12. 
B)  weaker than the bivariate correlation r12. 
C)  the same as the bivariate correlation r12. 
D)  uncertain. 
A)  stronger than the bivariate correlation r12. 
B)  weaker than the bivariate correlation r12. 
C)  the same as the bivariate correlation r12. 
D)  uncertain.

Question 14

An interaction between X1 and X2 is present in which of the following situations?

Accepted Answer

A)  The relationship between GPA (Y) and the time spent on watching TV (X1) is similar for students with different SAT scores (X2). 
B)  The relationship between GPA (Y) and the time spent on watching TV (X1) is different for students with higher SAT scores versus those with lower SAT scores (X2). 
C)  There is a strong correlation between the time spent on watching TV (X1) and SAT scores (X2). 
D)  There is a strong correlation between GPA (Y) and the time spent on watching TV (X1) controlling for SAT scores (X2). 
A)  The relationship between GPA (Y) and the time spent on watching TV (X1) is similar for students with different SAT scores (X2). 
B)  The relationship between GPA (Y) and the time spent on watching TV (X1) is different for students with higher SAT scores versus those with lower SAT scores (X2). 
C)  There is a strong correlation between the time spent on watching TV (X1) and SAT scores (X2). 
D)  There is a strong correlation between GPA (Y) and the time spent on watching TV (X1) controlling for SAT scores (X2).

Question 15

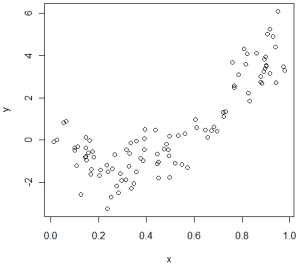The scatterplot of X and Y are shown as below.
  Based on the plot, which model is the most appropriate to use?

Accepted Answer

A)  Yi = b1Xi + a + ei. 
B)  Yi = b1Xi + b2Xi2 + a + ei. 
C)  Yi = b1Xi2 + a + ei. 
D)  Yi = b1Xi + b2Xi + b3Xi3 + a + ei. 
A)  Yi = b1Xi + a + ei. 
B)  Yi = b1Xi + b2Xi2 + a + ei. 
C)  Yi = b1Xi2 + a + ei. 
D)  Yi = b1Xi + b2Xi + b3Xi3 + a + ei.

Question 16

Which of the following statements about R2 and Radj2 is correct?

Accepted Answer

A)  R2 is always larger than Radj2. 
B)  R2 will always increase as more predictors are added to the model. 
C)  Radj2 adjusts for the number of independent variables and sample size. 
D)  If an additional independent variable were entered in the model, an increase in R2 indicates the new variable is adding value to the model. 
E)  R2 and Radj2 will never be negative. 
A)  R2 is always larger than Radj2. 
B)  R2 will always increase as more predictors are added to the model. 
C)  Radj2 adjusts for the number of independent variables and sample size. 
D)  If an additional independent variable were entered in the model, an increase in R2 indicates the new variable is adding value to the model. 
E)  R2 and Radj2 will never be negative.

Question 17

For the regression model, Yi = b1X1i + b2X2i + a + ei, consider the following two situations:
Situation 1: rY1 = -0.5 rY2 = 0.8 r12 = 0.1
Situation 2: rY1 = -0.5 rY2 = 0.8 r12 = 0.3
In which of the two situations will R2 be larger?

Accepted Answer

A)  situation 1. 
B)  situation 2. 
C)  R2 will be the same in both situations. 
D)  uncertain. 
A)  situation 1. 
B)  situation 2. 
C)  R2 will be the same in both situations. 
D)  uncertain.

Question 18

Which of the following situations will result in the best prediction in multiple regression analysis?

Accepted Answer

A)  rY1 = 0.1 rY2 = 0.4 r12 = 0.1 
B)  rY1 = 0.1 rY2 = 0.4 r12 = 0.8 
C)  rY1 = 0.6 rY2 = 0.4 r12 = 0.1 
D)  rY1 = 0.6 rY2 = 0.4 r12 = 0.8 
A)  rY1 = 0.1 rY2 = 0.4 r12 = 0.1 
B)  rY1 = 0.1 rY2 = 0.4 r12 = 0.8 
C)  rY1 = 0.6 rY2 = 0.4 r12 = 0.1 
D)  rY1 = 0.6 rY2 = 0.4 r12 = 0.8

Question 19

In a multiple regression model, Y is predicted from X1, X2, and X3. Both R2 and Radj2 are computed. If X3 is removed from the model, how will Radj2 change?

Accepted Answer

A)  Radj2 will increase. 
B)  Radj2 will decrease. 
C)  Radj2 will not change. 
D)  uncertain. 
A)  Radj2 will increase. 
B)  Radj2 will decrease. 
C)  Radj2 will not change. 
D)  uncertain.

Question 20

The multiple regression model for predicting Y from X1, X2, and X3 is
Yi = b1X1i + b2X2i + b3X3i + a + ei. If the bivariate correlation of Y and X1 is positive (rY1 > 0), the partial slope for X1 (b1) will be

Accepted Answer

A)  a positive value. 
B)  a negative value. 
C)  zero. 
D)  uncertain. 
A)  a positive value. 
B)  a negative value. 
C)  zero. 
D)  uncertain.

All of the following are possible effects of multicollinearity except

Calculate the partial correlation r_12.3 and the part correlation r_1(2.3) from the following bivariate correlations: r₁₂ = .3, r₁₃ = -.5, r23 = -.8.

The correlation between temperature (X₁) and the consumption of ice cream (X₂) controlling for price of ice cream (X₃) can be denoted by

The correlation of GPA (X₁) and the number of hours spent on watching TV (X₂) where the influence of IQ (X₃) is removed from GPA only can be denoted by

In a multiple regression model, Y is predicted from X₁, X₂, and X₃. Both R² and R_adj² are computed. If X₃ is removed from the model, how will R² change?

An interaction between X₁ and X₂ is present in which of the following situations?

The scatterplot of X and Y are shown as below. Based on the plot, which model is the most appropriate to use?

Which of the following statements about R² and R_adj² is correct?

For the regression model, Y_i = b₁X₁_i + b₂X₂_i + a + e_i, consider the following two situations: Situation 1: r_Y₁ = -0.5 r_Y₂ = 0.8 r₁₂ = 0.1 Situation 2: r_Y₁ = -0.5 r_Y₂ = 0.8 r₁₂ = 0.3 In which of the two situations will R² be larger?

Which of the following situations will result in the best prediction in multiple regression analysis?

In a multiple regression model, Y is predicted from X₁, X₂, and X₃. Both R² and R_adj² are computed. If X₃ is removed from the model, how will R_adj² change?

The multiple regression model for predicting Y from X₁, X₂, and X₃ is Y_i = b₁X₁_i + b₂X₂_i + b₃X₃_i + a + e_i. If the bivariate correlation of Y and X₁ is positive (r_Y₁> 0), the partial slope for X₁ (b₁) will be

Introduction

Data Representation

Univariate Population Parameters and Sample Statistics

Normal Distribution and Standard Scores

Introduction to Probability and Sample Statistics

Inferences About a Single Mean

Inferences About the Difference Between Two Means

Inferences About Proportions

Inferences About Variances

Bivariate Measures of Association

One-Factor Anova: Fixed-Effects Model

Multiple Comparison Procedures

Factorial Anova: Fixed-Effects Model

One-Factor Fixed-Effects Ancova With Single Covariate

Random- and Mixed-Effects Analysis of Variance Models

Hierarchical and Randomized Block Analysis of Variance Models

Simple Linear Regression

Logistic Regression

Filters

Exam 18: Multiple Regression

All of the following are possible effects of multicollinearity except

Calculate the partial correlation r12.3 and the part correlation r1(2.3) from the following bivariate correlations: r12 = .3, r13 = -.5, r23 = -.8.

The correlation between temperature (X1) and the consumption of ice cream (X2) controlling for price of ice cream (X3) can be denoted by

The correlation of GPA (X1) and the number of hours spent on watching TV (X2) where the influence of IQ (X3) is removed from GPA only can be denoted by

In a multiple regression model, Y is predicted from X1, X2, and X3. Both R2 and Radj2 are computed. If X3 is removed from the model, how will R2 change?

Carol is studying the correlation of college GPA (X1) and the number of hours spent on watching TV (X2). As intelligence is expected to affect GPA, she would like to remove the influence of IQ (X3) from GPA scores when computing the correlation. This is an example of which one of the following?

Suppose for the three variables, GPA (X1), time spent on watching TV (X2), and IQ (X3), the bivariate correlation coefficients are computed as below: R12 = -0.4; r13 = 0.6; r23 = 0. If we remove the influence of IQ from GPA, the correlation of GPA and the time spent on watching TV will be

An interaction between X1 and X2 is present in which of the following situations?

The scatterplot of X and Y are shown as below. Based on the plot, which model is the most appropriate to use?

Which of the following statements about R2 and Radj2 is correct?

For the regression model, Yi = b1X1i + b2X2i + a + ei, consider the following two situations: Situation 1: rY1 = -0.5 rY2 = 0.8 r12 = 0.1 Situation 2: rY1 = -0.5 rY2 = 0.8 r12 = 0.3 In which of the two situations will R2 be larger?

Which of the following situations will result in the best prediction in multiple regression analysis?

In a multiple regression model, Y is predicted from X1, X2, and X3. Both R2 and Radj2 are computed. If X3 is removed from the model, how will Radj2 change?

The multiple regression model for predicting Y from X1, X2, and X3 is Yi = b1X1i + b2X2i + b3X3i + a + ei. If the bivariate correlation of Y and X1 is positive (rY1 > 0), the partial slope for X1 (b1) will be

Introduction

Data Representation

Univariate Population Parameters and Sample Statistics

Normal Distribution and Standard Scores

Introduction to Probability and Sample Statistics

Inferences About a Single Mean

Inferences About the Difference Between Two Means

Inferences About Proportions

Inferences About Variances

Bivariate Measures of Association

One-Factor Anova: Fixed-Effects Model

Multiple Comparison Procedures

Factorial Anova: Fixed-Effects Model

One-Factor Fixed-Effects Ancova With Single Covariate

Random- and Mixed-Effects Analysis of Variance Models

Hierarchical and Randomized Block Analysis of Variance Models

Simple Linear Regression

Logistic Regression

Filters

Calculate the partial correlation r_12.3 and the part correlation r_1(2.3) from the following bivariate correlations: r₁₂ = .3, r₁₃ = -.5, r23 = -.8.

The correlation between temperature (X₁) and the consumption of ice cream (X₂) controlling for price of ice cream (X₃) can be denoted by

The correlation of GPA (X₁) and the number of hours spent on watching TV (X₂) where the influence of IQ (X₃) is removed from GPA only can be denoted by

In a multiple regression model, Y is predicted from X₁, X₂, and X₃. Both R² and R_adj² are computed. If X₃ is removed from the model, how will R² change?

An interaction between X₁ and X₂ is present in which of the following situations?

Which of the following statements about R² and R_adj² is correct?

For the regression model, Y_i = b₁X₁_i + b₂X₂_i + a + e_i, consider the following two situations: Situation 1: r_Y₁ = -0.5 r_Y₂ = 0.8 r₁₂ = 0.1 Situation 2: r_Y₁ = -0.5 r_Y₂ = 0.8 r₁₂ = 0.3 In which of the two situations will R² be larger?

In a multiple regression model, Y is predicted from X₁, X₂, and X₃. Both R² and R_adj² are computed. If X₃ is removed from the model, how will R_adj² change?

The multiple regression model for predicting Y from X₁, X₂, and X₃ is Y_i = b₁X₁_i + b₂X₂_i + b₃X₃_i + a + e_i. If the bivariate correlation of Y and X₁ is positive (r_Y₁> 0), the partial slope for X₁ (b₁) will be