Exam 13: Factorial Anova: Fixed-Effects Model
Exam 1: Introduction30 Questions
Exam 2: Data Representation30 Questions
Exam 3: Univariate Population Parameters and Sample Statistics30 Questions
Exam 4: Normal Distribution and Standard Scores30 Questions
Exam 5: Introduction to Probability and Sample Statistics30 Questions
Exam 6: Inferences About a Single Mean30 Questions
Exam 7: Inferences About the Difference Between Two Means30 Questions
Exam 8: Inferences About Proportions30 Questions
Exam 9: Inferences About Variances30 Questions
Exam 10: Bivariate Measures of Association30 Questions
Exam 11: One-Factor Anova: Fixed-Effects Model30 Questions
Exam 12: Multiple Comparison Procedures30 Questions
Exam 13: Factorial Anova: Fixed-Effects Model30 Questions
Exam 14: One-Factor Fixed-Effects Ancova With Single Covariate30 Questions
Exam 15: Random- and Mixed-Effects Analysis of Variance Models30 Questions
Exam 16: Hierarchical and Randomized Block Analysis of Variance Models30 Questions
Exam 17: Simple Linear Regression35 Questions
Exam 18: Multiple Regression29 Questions
Exam 19: Logistic Regression30 Questions
Select questions type
Complete the following ANOVA summary table for a two-factor fixed-effects ANOVA, where there are three levels of factor A (teaching method) and two levels of factor B (time of class). Each cell includes six students and = .05.
Source SS df MS F Critical Value Decision A 6.5 B 5.2 Within 39 Total 65
Free
(Essay)
4.8/5  (33)
(33)
Correct Answer:
There are 3 levels of factor A, so J = 3. There are 2 levels of factor B, so K = 2. Each cell has 6 students, so n = 6. N = 3*2*6 = 36.
dfA = J - 1 = 3 - 1 = 2, dfB = K - 1 = 2 - 1 = 1, dfAB = (J - 1)(K - 1) = 2*1 = 2,
dfwith = N - JK = 36 - 3*2 = 30, dftotal = N - 1 = 36 - 1 = 35.
SSA = dfA*MSA = 2*6.5 = 13, SSAB = dfAB*MSAB = 2*5.2 = 10.4,
SSB = SStotal - SSA - SSAB - SSwith = 65 - 13 - 10.4 - 39 = 2.6.
MSB = SSB/dfB = 2.6/1 = 2.6; MSwith = SSwith/dfwith = 39/30 = 1.3.
FA = MSA/MSwith = 6.5/1.3 = 5; critical value = .05F2,30 = 3.32 < FA, reject H0.
FB=MSB/MSwith = 2.6/1.3 = 2; critical value = .05F1,30 = 4.17 > FB, fail to reject H0.
FAB =MSAB/MSwith =5.2/1.3 = 4; critical value = .05F2,30 = 3.32 < FAB, reject H0.
based on the following ANOVA summary table (fixed effects):
Source df MS F 2 15 3.0 3 10 2.0 6 3 0.6 Within 120 5
-How many cells are there in the design?
Free
(Multiple Choice)
4.9/5  (40)
(40)
Correct Answer:
D
based on the following ANOVA summary table (fixed effects):
Source df MS F 5 18.0 6.0 1 13.5 4.5 5 15.0 5.0 Within 60 3.0
-How many cells are there in the design?
Free
(Multiple Choice)
4.8/5  (40)
(40)
Correct Answer:
C
based on the following ANOVA summary table (fixed effects):
Source df MS F 5 18.0 6.0 1 13.5 4.5 5 15.0 5.0 Within 60 3.0
-For which source of variation is the null hypothesis rejected at the .05 level of significance?
(Multiple Choice)
4.9/5  (39)
(39)
A researcher wanted to examine the effects of types of diet (factor A) and the age (factor B) on the weight gains of sheep. Diet type has four levels (i.e., four types of diet) and age has two levels (younger than one year old and older than one year old). Five sheep were assigned to each of the eight cells. The following are the scores (weight gains) from the individual cells:
A1B1: 11.8, 11.7, 11.1, 10.7, 10.4
A1B2: 11.1, 9.8, 9.5, 9.2, 8.8
A2B1: 10.2, 10.0, 8.7, 8.1, 7.3
A2B2: 8.6, 8.2, 7.7, 7.4, 5.6
A3B1: 12.0, 10.8, 10.5, 10.2, 10.2
A3B2: 10.7, 9.8, 9.7, 9.5, 8.9
A4B1: 9.8, 9.6, 9.4, 9.1, 7.9
A4B2: 8.0, 7.4, 7.4, 6.7, 5.8
Use SPSS to conduct a two-factor fixed-effects ANOVA to determine if there are any effects due to diet type, diet amount, or the interaction ( = 0.05). Conduct Tukey HSD post hoc comparisons, if necessary. (Presume all assumptions of ANOVA are satisfied.)
(Essay)
4.8/5  (28)
(28)
In a two-factor fixed-effects ANOVA, the interaction effect is definitely not present when
(Multiple Choice)
4.9/5  (33)
(33)
In a three-factor fixed-effects ANOVA, the three-way interaction effect is found to be significant. Which of the following statements is always true?
(Multiple Choice)
4.7/5  (34)
(34)
In a two-factor ANOVA, dfA = 2, dfB = 3, and each cell has five observations. what is dfAB?
(Multiple Choice)
4.8/5  (39)
(39)
A researcher used ANOVA to examine the effects of different types of diet on the weight gains of sheep. Specifically, he wants to see if the effect of diet type is different for sheep of different ages. Ten sheep were assigned to each of the four diet groups. Within each diet group, half of the sheep were younger than one year old, and the other half were older than one year old. How many factors are in this experiment and how many levels do these factors have?
(Multiple Choice)
4.9/5  (36)
(36)
based on the following plots of cell means. Assume that the within-cell variation is very small.
1) 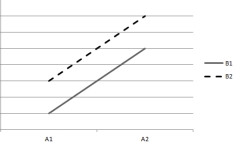 2)
2) 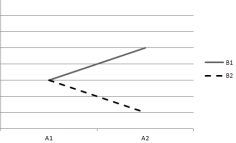 3)
3) 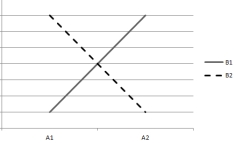 4)
4) 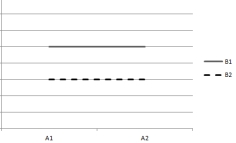 -Which plot indicates that both main effects are significant but the interaction effect is nonsignificant?
-Which plot indicates that both main effects are significant but the interaction effect is nonsignificant?
(Multiple Choice)
4.7/5  (38)
(38)
Complete the following ANOVA summary table for a two-factor fixed-effects ANOVA, where there are two levels of factor A (type of counseling) and four levels of factor B (frequency of counseling). Each cell includes six people and = .01.
Source SS df MS F Critical Value Decision 60 6 60 Within Total 640
(Essay)
4.8/5  (34)
(34)
Using the same data set (J = 3, K = 2, n = 10), Jane conducted two one-factor ANOVA, whereas Joe conducted a two-factor ANOVA. Which of the following statements is not true?
(Multiple Choice)
4.9/5  (31)
(31)
In a two-factor fixed-effects ANOVA, FA = 3, FB = 3.5, dfA = 3, dfB = 3. If the null hypothesis for factor A is rejected at .05 level of significance, the null hypothesis for factor B will be
(Multiple Choice)
4.9/5  (38)
(38)
In a two-factor ANOVA, dfA = 2, dfB = 3, and each cell has five observations. what is dfwith?
(Multiple Choice)
4.9/5  (34)
(34)
Which of the following situations would result in the greatest generalizability of the main effect for factor B across the levels of factor A?
(Multiple Choice)
4.8/5  (32)
(32)
A small-scale taste test is conducted to find out how the levels of moisture (factor A) and sweetness (factor B) of the cakes are related to people's preference to the cake. Participants' gender (factor C) is also considered. Each factor consists of two levels. Thirty-two participants are assigned to eight cells (i.e., four per cell), one for each of the factor combinations. The following are the scores (rating of the cakes by the participants) from the individual cells:
A1B1C1: 64, 61, 65, 70
A1B1C2: 63, 60, 64, 68
A1B2C1: 73, 76, 72, 71
A1B2C2: 72, 75, 79, 77
A2B1C1: 72, 78, 81, 75
A2B1C2: 74, 73, 75, 69
A2B2C1: 98, 97, 93, 89
A2B2C2: 86, 93, 88, 94
Use SPSS to conduct a three-factor fixed-effects ANOVA ( = 0.01). If there is (are) any significant interaction(s), graph and interpret the interaction(s).
(Essay)
4.8/5  (29)
(29)
The results of a two-factor ANOVA (J = 3, K = 2) show that both main effects are significant, but the interaction is not significant. We need to
(Multiple Choice)
4.9/5  (28)
(28)
based on the following plots of cell means. Assume that the within-cell variation is very small.
1)  2)
2)  3)
3)  4)
4)  -Which plot(s) indicate(s) significant interaction effects?
-Which plot(s) indicate(s) significant interaction effects?
(Multiple Choice)
4.9/5  (35)
(35)
based on the following ANOVA summary table (fixed effects):
Source df MS F 5 18.0 6.0 1 13.5 4.5 5 15.0 5.0 Within 60 3.0
-The total sample size for the design is which one of the following?
(Multiple Choice)
4.7/5  (34)
(34)
Showing 1 - 20 of 30
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)