Exam 11: Additional Topics and Applications
Exam 1: Systems of Linear Equations57 Questions
Exam 2: Euclidean Space48 Questions
Exam 3: Matrices76 Questions
Exam 4: Subspaces60 Questions
Exam 5: Determinants48 Questions
Exam 6: Eigenvalues and Eigenvectors75 Questions
Exam 7: Vector Spaces45 Questions
Exam 8: Orthogonality75 Questions
Exam 9: Linear Transformations60 Questions
Exam 10: Inner Product Spaces45 Questions
Exam 11: Additional Topics and Applications75 Questions
Select questions type
Verify that the given matrix A is normal, then diagonalize A by finding a unitary matrix P and diagonal matrix D such that
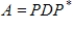 .
.
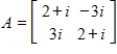
(Essay)
4.8/5  (37)
(37)
Find the maximum and minimum values of the quadratic form
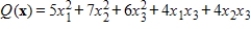 subject to the constraints
subject to the constraints
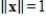 and
and
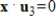 , where
, where
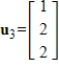 .
.
(Short Answer)
4.8/5  (28)
(28)
Show that the given matrix is positive definite, and then find the LDU-factorization.
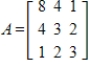
(Essay)
4.7/5  (30)
(30)
Find the maximum and minimum values of the quadratic form
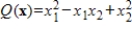 subject to the constraint
subject to the constraint
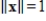 .
.
(Essay)
4.8/5  (31)
(31)
If B is any
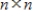 matrix, then the formula
matrix, then the formula
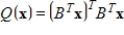 defines a positive semidefinite quadratic form on
defines a positive semidefinite quadratic form on
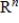 .
.
(True/False)
5.0/5  (37)
(37)
If m is the minimum value of a quadratic form
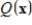 subject to the constraint
subject to the constraint
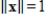 , then cm is the minimum value of
, then cm is the minimum value of
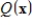 subject to the constraint
subject to the constraint
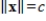 .
.
(True/False)
4.9/5  (37)
(37)
If A is positive definite, every entry along the diagonal of A is positive.
(True/False)
4.9/5  (32)
(32)
If the quadratic form
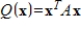 is positive definite, then A is invertible.
is positive definite, then A is invertible.
(True/False)
4.7/5  (41)
(41)
If A and B are
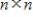 matrices that are both normal, and
matrices that are both normal, and
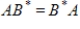 , then both
, then both
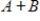 and AB are normal.
and AB are normal.
(True/False)
4.9/5  (33)
(33)
Show that the given matrix is positive definite, and then find the LDU-factorization of the matrix.
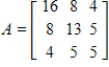
(Essay)
4.9/5  (34)
(34)
A symmetric matrix
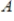 is positive definite if and only if
is positive definite if and only if
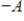 is negative definite.
is negative definite.
(True/False)
4.8/5  (30)
(30)
Showing 41 - 60 of 75
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)