Exam 6: Analysis of Variance, and Hypothesis Testing With Categorical Data: Chi Square

Correct Answer:

Verified

a. IV = level of self-control (ordinal).
DV = ever in contact with the criminal justice system (nominal).
b.
$$\begin{array} { | l | l | l | r | } \hline & \begin{array} { l } \text { Low self- } \\\text { control }\end{array} & \begin{array} { l } \text { High self- } \\\text { control }\end{array} & \\\hline & \mathrm { A } & \mathrm { B } & 126 \\\text { Yes } & 57 ( 47.5 \% ) & 69 ( 30 \% ) & ( 36 \% ) \\\hline & \mathrm { C } & \mathrm { D } & 224\\\text { No } & 63 ( 52.5 \% ) & 161 ( 70 \% ) & \begin{array} { r } \\( 64 \% )\end{array} \\\hline && & 350 \\& 120 ( 100 \% ) & 230 ( 100 \% ) & ( 100 \% ) \\\hline\end{array}$$
c. H₀: There is no relationship between one's level of self-control and criminal behavior.
H₁: There is a relationship between one's level of self-control and criminal behavior.
d. df = (c - 1)(r - 1) = (2 - 1)(2 - 1) = 1.
e. You reject the null hypothesis if x² is greater than 3.841.
f. E(A) = (120 × 126)/350 = 43.2
E(B) = (230 × 126)/350 = 82.8
E(C) = (120 × 224)/350 = 76.8
E(D) = (230 × 224)/350 = 147.2
g.
$$\chi ^ { 2 } = \Sigma \frac { ( O - E ) ^ { 2 } } { E } = 10.482$$
$\begin{array}{|l|c|c|r|r|r|}\hline&&&&{(O-} & {(O-}\\ \text { Cell } & O & E & O-E &E)^{\mathbf{2}} &{E)^{\mathbf{2}} / E} \\ \hline \mathrm{A} & 57 & 43.2 & 13.8 & 190.44 & 4.408 \\\hline \mathrm{B} & 69 & 82.8 & -13.8 & 190.44 & 2.300 \\\hline \mathrm{C} & 63 & 76.8 & -13.8 & 190.44 & 2.480 \\\hline \mathrm{D} & 161 & 147.2 & 13.8 & 190.44 & 1.294 \\\hline & & & & \sum & 10.482 \\\hline\end{array}$

h. You reject the null hypothesis (alpha 0.05) because x² (10.48) is greater than 3.841, meaning that there is a statistically significant relationship between one's level of self-control and criminal behavior, χ²(1) = 10.48, p < 0.05. Although 47.5% of high school students with a low level of self-control have been in contact with the criminal justice system, only 30% of high-school students with a high level of self-control have been. You select an alpha level of 0.05.

Correct Answer:

Verified

a. IV = gender: male, female, transgender (nominal).
DV = legal status: legalize, decriminalize, criminalize (nominal).
b.

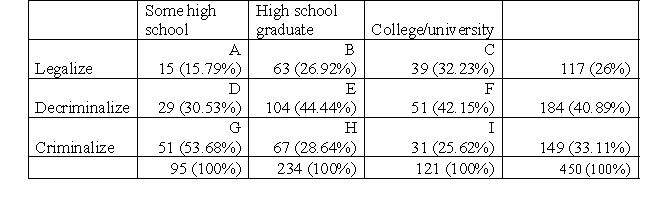
c. H₀: There is no relationship between one's level of education and one's attitudes toward the legal status of prostitution (legalize, decriminalize, criminalize).
H₁: There is a relationship between one's level of education and one's attitudes toward the legal status of prostitution (legalize, decriminalize, criminalize).
d. df = (c - 1)(r - 1) = (3 - 1)(3 - 1) = 4.
e. You reject the null hypothesis if x² is greater than 9.488.
f. E(A) = (95 × 117)/450 = 24.7
E(B) = (234 × 117)/450 = 60.84
E(C) = (121 × 117)/450 = 31.46
E(D) = (95 × 184)/450 = 38.84
E(E) = (234 × 184)/450 = 95.68
E(F) = (121 × 184)/450 = 49.48
E(G) = (95 × 149)/450 = 31.46
E(H) = (234 × 149)/450 = 77.48
E(I) = (121 × 149)/450 = 40.06
g.
$$\chi ^ { 2 } = \Sigma \frac { ( O - E ) ^ { 2 } } { E } = 24.559$$
$\begin{array}{|l|r|r|r|r|r|}\hline&&&&& (O- \\ \text { Cell } & O & E&O-E & (O-E)^{2}&E^{2} / E \\ \hline \mathrm{A} & 15 & 24.7 & -9.7 & 94.09 & 3.809 \\\hline \mathrm{B} & 63 & 60.84 & 2.16 & 4.6656 & 0.077 \\\hline \mathrm{C} & 39 & 31.46 & 7.54 & 56.8516 & 1.807 \\\hline \mathrm{D} & 29 & 38.84 & -9.84 & 96.8256 & 2.493 \\\hline \mathrm{E} & 104 & 95.68 & 8.32 & 69.2224 & 0.723 \\\hline \mathrm{F} & 51 & 49.48 & 1.52 & 2.3104 & 0.047 \\\hline \mathrm{G} & 51 & 31.46 & 19.54 & 381.8116 & 12.136 \\\hline \mathrm{H} & 67 & 77.48 & -10.48 & 109.8304 & 1.418 \\\hline \mathrm{I} & 31 & 40.06 & -9.06 & 82.0836 & 2.049 \\\hline & & & & \sum & 24.559 \\\hline\end{array}$

h. You reject your null hypothesis because χ²(4) = 24.599, p > 0.05. There is a statistically significant relationship between level of education and attitudes toward the legal status of prostitution. Whereas 15.79% of individuals with some high school are in favor of legalizing prostitution, 26.92% of high school graduates and 32.23% of college/university students are. Also, whereas only 25.62% of college/university students and 28.64% of high school graduates are in favor of keeping prostitution illegal, 53.68 of individuals with some high school education are pro-criminalization.

Correct Answer:

Verified

a. The appropriate test of association is phi $$\phi = \sqrt { \frac { \chi ^ { 2 } } { n } }$$
b. $$\begin{array} { l } \text { i. } \chi ^ { 2 } = 4.235 ; n = 153 \text {. } \\\phi = \sqrt { \frac { 4.235 } { 153 } } = 0.17 \\\end{array}$$
17% of the variance within the DV variable is explained by the IV, leaving 83% of the variance unexplained (explained by other variables).
$$\begin{array} { l } \text { ii. } \chi ^ { 2 } = 18.567 ; n = 215 \\- \phi = \sqrt { \frac { 18.567 } { 215 } } = 0.29\end{array}$$
29% of the variance within the DV variable is explained by the IV, leaving 71% of the variance unexplained (explained by other variables).
iii. $$\begin{array} { l } \chi ^ { 2 } = 3.898 ; n = 310 \\\phi = \sqrt { \frac { 3.898 } { 310 } } = 0.11\end{array}$$ 11% of the variance within the DV variable is explained by the IV, leaving 89% of the variance unexplained (explained by other variables).
iv. $\quad \chi ^ { 2 } = 22.33 ; n = 146$ .
$$\phi = \sqrt { \frac { 22.33 } { 146 } } = 0.39$$
39% of the variance within the DV variable is explained by the IV, leaving 61% of the variance unexplained (explained by other variables).
v. χ² = 10.659; n = 189.
$$\phi = \sqrt { \frac { 10.659 } { 189 } } = 0.24$$
24% of the variance within the DV variable is explained by the IV, leaving 76% of the variance unexplained (explained by other variables).
$$\begin{array} { l } \text { i. } \chi ^ { 2 } = 29.66 ; n = 195 \text {. } \\\phi = \sqrt { \frac { 29.66 } { 195 } } = 0.39\end{array}$$
vi.
39% of the variance within the DV variable is explained by the IV, leaving 61% of the variance unexplained (explained by other variables).