Exam 7: Theoretical Distributions Including the Normal Distribution

Here are some items that were great fun when the movie, Star Wars first came out (1977). Some problems, of course, are classics.The following questions were received in last week's time capsule. May the Force be with you. a. On the average, it takes Han Solo 45 seconds to check the coordinates and make the jump into hyperspace. The standard deviation on this important task is 5 seconds. When Han and Chewbacca and their passengers are leaving for Alderaan they must make the jump in 33 seconds or less. What is the probability of such an accomplishment? b. In a space bar there were 14 storm troopers, 3 Wookies, 9 humans, and 2 scriptwriters. An Android entered, fired a shot, and hit someone in the cheek. What is the probability that a scriptwriter was hit (and won't have anyplace to put his tongue)? c. Jawas, those jewel-eyed, hooded collectors of robots and scrap, live in the desert and travel by sandcrawler. Their height is normally distributed with a mean of four feet and a standard deviation of 3 inches. The escape exit on the sandcrawler is 46 inches high. What proportion of the Jawas must duck when they use the escape exit? d. The Head Jawa, a sleepy-eyed fellow with neurons to match, took a psychology course but got things jumbled up. He concluded that the extreme five percent of a population should not be counted as part of that population. He went home to the rocks, counted his people, and sent those whose heights put them in the extreme five percent to Alderaan. If there were 600 people to begin with, how many were banished and what were their heights? e. Darth Vader has a distinct respiratory mannerism. This mannerism is so noticeable that the Dark Lord of the Sith can be heard by an average R-2 droid (a classification that certainly does not include Artoo Detoo) who is 18 meters away. The standard deviation of this detection task is 50 centimeters. Suppose that 60 R-2s were 18 meters from a door that Darth Vader walked through. How many of these R-2s would be expected to know that the one who represents the dark side of the Force has entered? f. According to Obi-Wan Kenobe, the last of the Jedi Knights, "The Force can have an influence on the weak-minded." Unfortunately for psychology, concepts like a weak mind have been abandoned and therefore psychologists cannot hope to understand this most important intervening variable. Please answer the following question which you will have no difficulty with; which you will answer quickly, completely, and correctly. The beautiful Princess Leia, in a prescience trance, saw a funny hair style on 1920s movie stars in America. She decided to adopt this hair style and practiced and practiced winding her hair in circles using her ears as cores. On the average she got 12 coils and the standard deviation was two coils. What is the probability that, on the day she was rescued by Luke, Han, and Chewey, she had between 11 and 14 coils?

Data Set 7-6, a theoretical distribution: 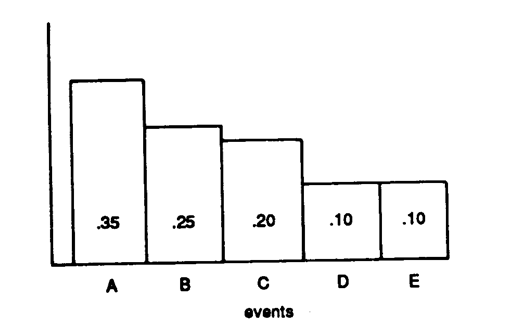-Look at Data Set 7-6. The probability of occurrence of Event B or Event E is

On the average it takes 27 throws to complete the College Frisbee Golf Course. The standard deviation about this mean is 4. a. What proportion of the population would be expected to score 22 or less (par)? b. What proportion would score between 25 and 30? c. If 950 students played and a prize was given to those who scored 20 or less, how many would get prizes? d. Suppose an experimenter wanted to find some very good and some very poor frisbee players to use in an experiment. She decided to use the top 10 percent and the bottom 10 percent from the CFGC. What are the cut-off scores? e. What proportion would be expected to score between 28 and 32? f. What assumption is being made about the nature of the distribution of frisbee golf scores in the questions above?

More than 1.5 million college-bound high school seniors took the Critical Reading portion of the SAT exam recently. The mean was 503; the standard deviation was 113. a. What proportion scored 500 or above? b. Suppose that a university, based on past experience, decided to not admit anyone whose Critical Reading score placed them in the lowest 20 percent of the population. What is that score? c. What proportion of the population scored between 600 and 700? d. From 1000 students, how many would be expected to score 700 or more? e. In working these problems, you began with an assumption about the distribution of Critical Reading test scores. What is that assumption?

The total area of each theoretical distribution described in Chapter 7 was 1.00.

Suppose the mean number of books in "County Libraries" is 10,000 and the standard deviation is 2,000. Assume the distribution is normal. a. What proportion of the libraries have between 6,000 and 8,500 books? b. How many books would a library have to have to be in the top 15 percent? c. Defend or attack the assumption that the distribution of books in "County Libraries" is normal.

Given below are lower and upper limits of an area of the normal curve. Choose the limits that contain the smallest proportion of the normal curve.

Which of the following is a theoretical distribution?

The mean and standard deviation of standard intelligence tests is

If an urn contains 2 red balls, 2 blue balls, and 1 green ball, the probability of drawing a green ball is .10.

The difference between an empirical distribution and a theoretical distribution is that a theoretical distribution

When your text compared the empirical results of IQ scores of fifth grade students with theoretical predictions based on the normal curve, the correspondence was good. The place where prediction was poorest was

Empirical distributions are not based on mathematics or logic.

The distribution not discussed in Chapter 7 was thedistribution.

More than 1.5 million college-bound high school seniors took the Mathematics portion of the SAT exam recently. The mean was 518; the standard deviation was 115. a. What proportion scored 600 or above? b. An engineering school decided to restrict admissions to those who scored in the top 15 percent. What is the cut off score? c. What proportion of the test takers scored between 400 and 500? d. From 1000 students, how many would be expected to score 700 or more? e. In working these problems, you began with an assumption about the distribution of SAT Mathematics test scores. What is that assumption?

.2580 of the normal curve lies between $\mu$ and .70 $\sigma$ . The proportion between $\mu$ and .35 $\sigma$ is

To use the theoretical normal curve, which of the following things must be known about the population?

Your text credits__________with developing the normal curve.

If an empirical distribution is converted to a distribution of z scores, the new

If an urn contains 2 red balls, 2 blue balls, and 1 green ball, the probability of drawing a red ball is .50.