Exam 6: Linear Transformations
Exam 1: Linear Equations25 Questions
Exam 2: Matrices48 Questions
Exam 3: Determinants47 Questions
Exam 4: Vector Spaces100 Questions
Exam 5: Inner Product Spaces54 Questions
Exam 6: Linear Transformations46 Questions
Exam 7: Eigenvalues Eigenvectors32 Questions
Select questions type
The standard matrix A for the linear transformation T, where T is the counterclockwise rotation of 45° about the origin in 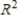 is given by
is given by 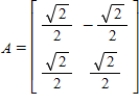 . Use the matrix A to find
. Use the matrix A to find 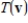 for the vector
for the vector 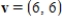 .
.
Free
(Multiple Choice)
4.9/5  (30)
(30)
Correct Answer:
A
Find the standard matrix A for the linear transformation T, where T is the counterclockwise rotation of 30° about the origin in 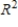 .
.
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
D
The linear transformation 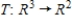 is defined by
is defined by 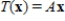 , where
, where 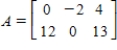 Find rank(T)
Find rank(T)
(Multiple Choice)
4.7/5  (30)
(30)
The linear thransformation 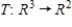 is represented by
is represented by 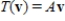 , where
, where 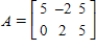 Find a basis for the kernel of T.
Find a basis for the kernel of T.
(Multiple Choice)
4.7/5  (22)
(22)
Identify the transformation 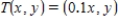 for an arbitrary vector
for an arbitrary vector 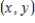 in the plane.
in the plane.
(Multiple Choice)
4.8/5  (35)
(35)
Let 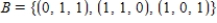 and
and 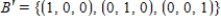 be bases for
be bases for 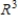 , and let
, and let 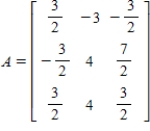 be the matrix for
be the matrix for 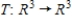 relative to B. The transition matrix P from B' to B is
relative to B. The transition matrix P from B' to B is 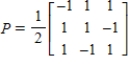 . Use the matrices A and P to find
. Use the matrices A and P to find 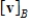 and
and 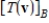 where
where 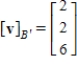 .
.
(Multiple Choice)
4.8/5  (21)
(21)
Let 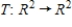 be the reflection in the x-axis. Find the image of the vector
be the reflection in the x-axis. Find the image of the vector 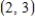 .
.
(Multiple Choice)
4.9/5  (32)
(32)
Let 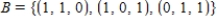 and
and 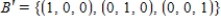 be bases for
be bases for 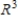 . Find the transition matrix P from B' to B.
. Find the transition matrix P from B' to B.
(Multiple Choice)
4.7/5  (32)
(32)
The linear transformation 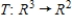 is defined by
is defined by 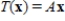 , where
, where 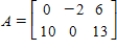 Find nullity(T).
Find nullity(T).
(Multiple Choice)
4.8/5  (32)
(32)
The vector v is a fixed point of T if 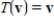 . Find all fixed points of the linear transformation T where T is the reflection in the line y = x.
. Find all fixed points of the linear transformation T where T is the reflection in the line y = x.
(Multiple Choice)
4.9/5  (46)
(46)
Find the kernel of the linear transformation 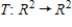 , defined by
, defined by 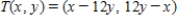 .
.
(Multiple Choice)
4.9/5  (32)
(32)
The linear transformation 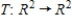 is defined by
is defined by 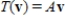 , where
, where 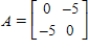 Find the preimage of (15, 15).
Find the preimage of (15, 15).
(Multiple Choice)
4.7/5  (38)
(38)
Let 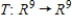 be a linear transformation. Find the nullity of T given that
be a linear transformation. Find the nullity of T given that 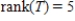 .
.
(Multiple Choice)
4.9/5  (38)
(38)
Sketch the image of the unit square with vertices at (0, 0), (1, 0), (1, 1), and (0, 1) under the transformation T which is the contraction given by 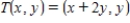 .
.
(Multiple Choice)
4.8/5  (29)
(29)
Showing 1 - 20 of 46
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)