Exam 7: Eigenvalues Eigenvectors
Exam 1: Linear Equations25 Questions
Exam 2: Matrices48 Questions
Exam 3: Determinants47 Questions
Exam 4: Vector Spaces100 Questions
Exam 5: Inner Product Spaces54 Questions
Exam 6: Linear Transformations46 Questions
Exam 7: Eigenvalues Eigenvectors32 Questions
Select questions type
Which of the following are eigenvalues with corresponding eigenvectors for the matrix 
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
A
Find the eigenvalues and corresponding eigenvectors for the matrix if the characteristic equation of the matrix is 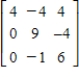 if the characteristic equation of the matrix is
if the characteristic equation of the matrix is 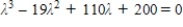 .
.
Free
(Multiple Choice)
4.9/5  (36)
(36)
Correct Answer:
C
Find an orthogonal matrix P such that 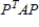 diagonalizes
diagonalizes 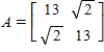 .
.
Free
(Multiple Choice)
4.9/5  (35)
(35)
Correct Answer:
E
Find a stable age distribution for the age transition matrix  .
.
(Multiple Choice)
4.9/5  (37)
(37)
Solve the system of first-order linear differential equations given below. 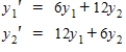
(Multiple Choice)
4.8/5  (31)
(31)
Find a basis 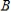 for the domain of
for the domain of 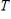 such that the matrix of
such that the matrix of 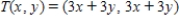 relative to
relative to 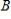 is diagonal.
is diagonal.
(Multiple Choice)
4.8/5  (28)
(28)
Use the Principal Axes Theorem to perform a rotation of axes to eliminate the xy-term in the quadratic equation 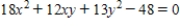 . Identify the resulting rotated conic and give its equation in the new coordinate system.
. Identify the resulting rotated conic and give its equation in the new coordinate system.
(Multiple Choice)
4.8/5  (39)
(39)
Use the age transition matrix 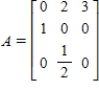 and age distribution vector
and age distribution vector 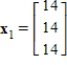 to find the age distribution vectors
to find the age distribution vectors  and
and  .
.
(Multiple Choice)
4.8/5  (28)
(28)
Find the eigenvalues and corresponding eigenvectors for the matrix 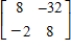 if the characteristic equation of the matrix is
if the characteristic equation of the matrix is 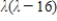 .
.
(Multiple Choice)
4.7/5  (33)
(33)
Find the eigenvalues and corresponding eigenvectors for the matrix 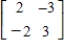 .
.
(Multiple Choice)
4.8/5  (33)
(33)
Find a stable age distribution for the age transition matrix 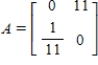 .
.
(Multiple Choice)
4.8/5  (42)
(42)
Suppose a population has the characteristics listed below.
(a) A total of 60% of the population survives its first year. Of that 60%, 50% survives the second year. The maximum life span is 3 years.
(b) The average number of offspring for each member of the population is 4 the first year, 5 the second year, and 4 the third year.The population now consists of 150 members in each of the three age class. How many members will be in each age class after one year? After two years? Let  , and
, and  be vectors whose components are the number members in each age class after one year and after two years respectively.
be vectors whose components are the number members in each age class after one year and after two years respectively.
(Multiple Choice)
4.9/5  (35)
(35)
Showing 1 - 20 of 32
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)