Exam 2: Matrices
Exam 1: Linear Equations25 Questions
Exam 2: Matrices48 Questions
Exam 3: Determinants47 Questions
Exam 4: Vector Spaces100 Questions
Exam 5: Inner Product Spaces54 Questions
Exam 6: Linear Transformations46 Questions
Exam 7: Eigenvalues Eigenvectors32 Questions
Select questions type
Which of the following is a product of elementary matrices for the matrix 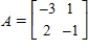
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
C
Use the following matrices to perform the indicated matrix operations, if possible. 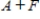
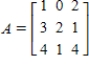 ,
, 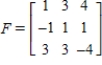
(Multiple Choice)
4.8/5  (33)
(33)
Use inverse matrices and the graphing calculator to find the solution of the system of equations. 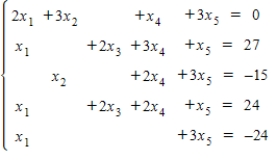
(Multiple Choice)
4.8/5  (40)
(40)
A system composed of two industries, coal and steel, has the inputs as seen below.(a) To produce 1 dollar's worth of output, the coal industry requires $0.30 of its own product and $0.70 of steel. (b) To produce 1 dollar's worth of output, the steel industry requires $0.30 of its own product and $0.10 of coal. Find D, the input-output matrix for this system. Then solve for the output matrix X in the equation 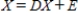 where the external demand is
where the external demand is 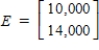 . Round all the entries of the matrix to two decimal places, where applicable.
. Round all the entries of the matrix to two decimal places, where applicable.
(Multiple Choice)
4.8/5  (28)
(28)
A small community includes a farmer, a baker, and a grocer and has the input-output matrix  and external demand matrix
and external demand matrix 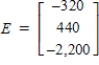 . Solve for the output matrix X in the equation
. Solve for the output matrix X in the equation 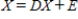 .
.
(Multiple Choice)
4.7/5  (38)
(38)
A population of 10,000 is grouped as follows: 5,000 nonsmokers, 3,500 smokers of one pack or less per day, and 1,500 smokers of more than one pack per day. During any month there is a 5% probability that a nonsmoker will begin smoking a pack or less per day, and a 4% probability that a nonsmoker will begin smoking more than a pack per day. For smokers who smoke a pack or less per day, there is a 10% probability of quitting and a 10% probability of increasing to more than a pack per day. For smokers who smoke more than a pack per day, there is a 5% probability of quitting and a 20% probability of dropping to a pack or less per day. How many people will be in each of the three groups in 1 month?
(Multiple Choice)
4.9/5  (34)
(34)
Use the matrices below. Perform the indicated operation.
AB 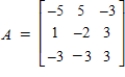 ,
, 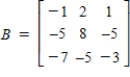
(Multiple Choice)
4.7/5  (37)
(37)
Suppose that the table shows the numbers y of motor vehicle registrations (in millions) in the United States for the years 2000 through 2004. Use the method of least squares to find the least squares regression line for the data. Let t represent the year, with corresponding to 2000. Round the coefficient and constant of the equation to two decimal places 
(Multiple Choice)
4.9/5  (30)
(30)
The market research department at a manufacturing plant determines that 30% of the people who purchase the plant's product during any month will not purchase it the next month. On the other hand, 40% of the people who do not purchase the product during any month will purchase it the next month. In a population of 1000 people, 100 people purchased the product this month. How many will purchase the product next month?
(Multiple Choice)
4.9/5  (35)
(35)
Use the following matrices to perform the indicated matrix operations, if possible. 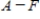
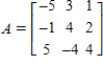 ,
, 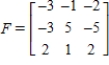
(Multiple Choice)
5.0/5  (43)
(43)
A population of 100,000 consumers is grouped as follows: 20,000 users of Brand A, 30,000 users of Brand B, and 50,000 who use neither brand. During any month a Brand A user has a 20% probability of switching to Brand B and a 10% probability of not using either brand. A Brand B user has a 15% probability of switching to Brand A and a 20% probability of not using either brand. A nonuser has a 20% probability of purchasing Brand A and a 25% probability of purchasing Brand B. How many people will be in each group in 1 month?
(Multiple Choice)
4.8/5  (25)
(25)
Showing 1 - 20 of 48
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)