Exam 1: Introduction
Exam 1: Introduction28 Questions
Exam 2: First-Order Differential Equations73 Questions
Exam 3: Second-Order Linear Differential Equations119 Questions
Exam 4: Higher-Order Linear Differential Equations54 Questions
Exam 5: Series Solutions of Second-Order Linear Equations81 Questions
Exam 6: The Laplace Transform57 Questions
Exam 7: Systems of First-Order Linear Equations97 Questions
Exam 8: Numerical Methods63 Questions
Exam 9: Nonlinear Differential Equations and Stability76 Questions
Exam 10: Partial Differential Equations and Fourier Series44 Questions
Exam 11: Boundary Value Problems and Sturm-Liouville Theory19 Questions
Select questions type
A portion of the direction field for the differential equation 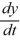 = f(y) is shown below:
= f(y) is shown below:
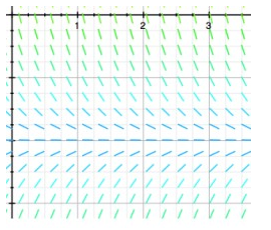 The dotted horizontal line has equation y = -7. Which of the following statements are true? Select all that apply.
The dotted horizontal line has equation y = -7. Which of the following statements are true? Select all that apply.
Free
(Multiple Choice)
4.8/5  (37)
(37)
Correct Answer:
B, E, F
Newton's Law of Cooling states that the temperature of an object changes at a rate proportional to the difference between the temperature of the object itself and the temperature of its surroundings (typically the ambient temperature). Suppose the ambient temperature is 72°F and the rate constant is 0.11 per minute.What is the general solution of the differential equation for the temperature of the object, T(t), at any time t?
Free
(Multiple Choice)
4.8/5  (31)
(31)
Correct Answer:
D
A model for the vertical flight of a projectile launched from the ground with velocity V in the absence of air resistance is
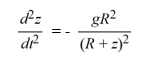 From what single term in this equation can you infer the order of the equation?
From what single term in this equation can you infer the order of the equation?
Free
(Essay)
4.8/5  (25)
(25)
Correct Answer:
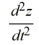
For what values of r is y(t) = 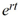 a solution of the differential equation
a solution of the differential equation 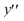 +4
+4 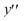 - 12y = 0?
- 12y = 0?
(Multiple Choice)
4.8/5  (35)
(35)
An antibiotic is being administered intravenously to a patient. Fluid containing 6.5 mg/ of the antibiotic enters the patient's bloodstream at a rate of 100 /hour. The antibiotic is absorbed by the body or otherwise leaves the bloodstream at a rate proportional to the amount present, with a rate constant of 0.4 per hour. Assume the antibiotic is always uniformly distributed throughout the bloodstream.Which of these is a differential equation for the amount of antibiotic, A(t), in the bloodstream at any time t?
(Multiple Choice)
4.7/5  (40)
(40)
Which of the following are solutions to the differential equation 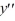 - 16y = 0? Select all that apply.
- 16y = 0? Select all that apply.
(Multiple Choice)
4.7/5  (35)
(35)
Consider the differential equation x = 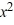 + y.What is the value of the constant C in the general solution corresponding to the initial condition y(2) = 0?
+ y.What is the value of the constant C in the general solution corresponding to the initial condition y(2) = 0?
(Short Answer)
4.9/5  (34)
(34)
Which of the following are solutions to the differential equation 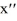 - 2
- 2 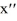 = 0? Select all that apply
= 0? Select all that apply
(Multiple Choice)
4.8/5  (30)
(30)
Eight differential equations and four slope fields are given below
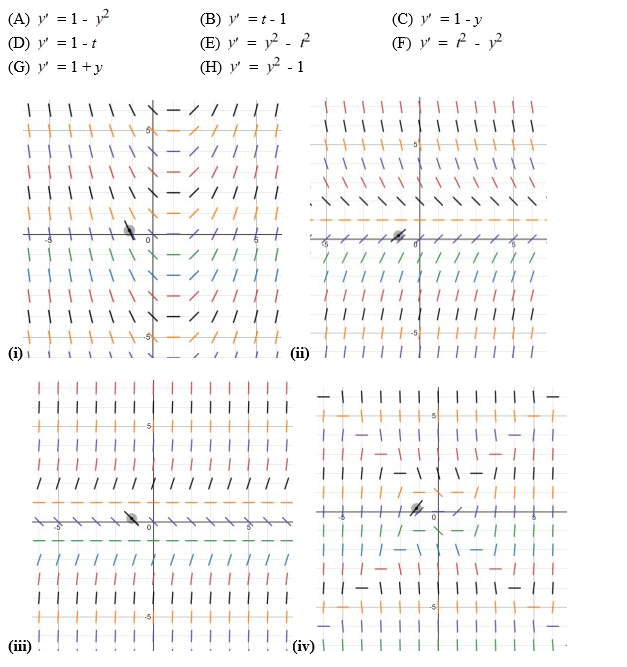 Which of the following are the zero isoclines for the differential equation in (A)? Select all that apply.
Which of the following are the zero isoclines for the differential equation in (A)? Select all that apply.
(Multiple Choice)
5.0/5  (41)
(41)
Which of the following pairs of values of A and B are such that all solutions of the differential equation 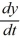 = Ay + B are such that
= Ay + B are such that 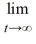 y(t) = 7?
Select all that apply.
y(t) = 7?
Select all that apply.
(Multiple Choice)
4.8/5  (36)
(36)
A model for the vertical flight of a projectile launched from the ground with velocity V in the absence of air resistance is
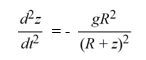 Is this differential equation linear or nonlinear?
Is this differential equation linear or nonlinear?
(Short Answer)
4.8/5  (28)
(28)
A pond initially contains 150,000 gallons of water and an unknown amount of pesticide. Water containing 0.08 grams of pesticide per gallon flows into the pond at a rate of 400 gallons per hour. The mixture flows out of the pond at the same rate, so the amount of water in the pond remains constant. Assume the pesticide is uniformly mixed throughout the pond.How much pesticide will be in the pond after a very long time? ________ grams.
(Short Answer)
4.9/5  (26)
(26)
A model for the vertical flight of a projectile launched from the ground with velocity V in the absence of air resistance is
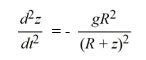 Which of these initial conditions complete the description of the situation? Select all that apply.
Which of these initial conditions complete the description of the situation? Select all that apply.
(Multiple Choice)
4.8/5  (31)
(31)
A pond initially contains 70,000 gallons of water and an unknown amount of pesticide. Water containing 0.07 grams of pesticide per gallon flows into the pond at a rate of 360 gallons per hour. The mixture flows out of the pond at the same rate, so the amount of water in the pond remains constant. Assume the pesticide is uniformly mixed throughout the pond.
Which of these is the differential equation for the amount of pesticide, P(t), in the pond at any time t?
(Multiple Choice)
4.9/5  (37)
(37)
Consider the differential equation x 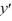 =
= 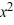 + y.
What is the general solution of this equation?
+ y.
What is the general solution of this equation?
(Multiple Choice)
4.9/5  (29)
(29)
Newton's Law of Cooling states that the temperature of an object changes at a rate proportional to the difference between the temperature of the object itself and the temperature of its surroundings (typically the ambient temperature). Suppose the ambient temperature is 77°F and the rate constant is 0.09 per minute.Which of these is a differential equation for the temperature of the object, T(t), at any time t?
(Multiple Choice)
4.7/5  (35)
(35)
For each of the following partial differential equations, identify the order and indicate whether it is linear or nonlinear.
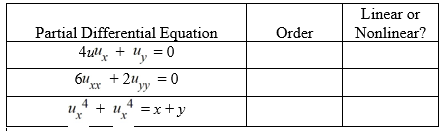
(Essay)
4.8/5  (39)
(39)
A pond initially contains 100,000 gallons of water and an unknown amount of pesticide. Water containing 0.07 grams of pesticide per gallon flows into the pond at a rate of 320 gallons per hour. The mixture flows out of the pond at the same rate, so the amount of water in the pond remains constant. Assume the pesticide is uniformly mixed throughout the pond.Which of these is the solution of the initial-value problem comprised of the differential equation for the amount of pesticide, P(t), in the pond at any time t and the initial condition P(0) = P0?
(Multiple Choice)
4.9/5  (33)
(33)
A pond initially contains 120,000 gallons of water and an unknown amount of pesticide. Water containing 0.08 grams of pesticide per gallon flows into the pond at a rate of 260 gallons per hour. The mixture flows out of the pond at the same rate, so the amount of water in the pond remains constant. Assume the pesticide is uniformly mixed throughout the pond.Which of these equations would you need to solve to find the time T (in hours) after which P(t) is within 2% of its limiting behavior?
(Multiple Choice)
4.8/5  (23)
(23)
An antibiotic is being administered intravenously to a patient. Fluid containing 4.5 mg/Cm3 of the antibiotic enters the patient's bloodstream at a rate of 100 Cm3/hour. The antibiotic is absorbed by the body or otherwise leaves the bloodstream at a rate proportional to the amount present, with a rate constant of 0.5 per hour. Assume the antibiotic is always uniformly distributed throughout the bloodstream.What is the general solution to the differential equation for the amount of antibiotic, A(t), in the bloodstream at any time t?
(Multiple Choice)
4.9/5  (32)
(32)
Showing 1 - 20 of 28
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)