Exam 3: Second-Order Linear Differential Equations
Exam 1: Introduction28 Questions
Exam 2: First-Order Differential Equations73 Questions
Exam 3: Second-Order Linear Differential Equations119 Questions
Exam 4: Higher-Order Linear Differential Equations54 Questions
Exam 5: Series Solutions of Second-Order Linear Equations81 Questions
Exam 6: The Laplace Transform57 Questions
Exam 7: Systems of First-Order Linear Equations97 Questions
Exam 8: Numerical Methods63 Questions
Exam 9: Nonlinear Differential Equations and Stability76 Questions
Exam 10: Partial Differential Equations and Fourier Series44 Questions
Exam 11: Boundary Value Problems and Sturm-Liouville Theory19 Questions
Select questions type
Consider the pair of functions y1 = t and y2 = 3t2.
Which of these statements are true? Select all that apply.
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
B, D
Compute the Wronskian of the pair of functions sin(5t) and cos(5t).
Free
(Multiple Choice)
4.9/5  (33)
(33)
Correct Answer:
A
Suppose a 6-lb object stretches a spring 2 feet while in equilibrium. If the object is displaced an additional 2.5 inches and is then set in motion with an initial upward velocity of -1 feet per second.
What is the natural frequency? Round your answer to the nearest hundredth radian per second.
Free
(Short Answer)
5.0/5  (34)
(34)
Correct Answer:
4.00 radians per second
For which of these differential equations is the characteristic equation given by 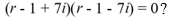
(Multiple Choice)
4.9/5  (45)
(45)
Suppose that Y1 and Y2 are both solutions of the differential equation 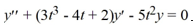 .
Which of the following must also be solutions of this differential equation? Select all that apply. Here, C1 , and C2 are arbitrary real constants.
.
Which of the following must also be solutions of this differential equation? Select all that apply. Here, C1 , and C2 are arbitrary real constants.
(Multiple Choice)
4.7/5  (31)
(31)
For which of these differential equations is the characteristic equation given by 6 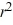 + 7 = 0?
+ 7 = 0?
(Multiple Choice)
4.8/5  (37)
(37)
Consider the nonhomogeneous differential equation 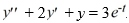 Assume that
Assume that 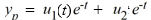 is a particular solution of this differential equation. Use variation of parameters to determine u1 (t) and u2 (t).
u1 (t) = ________ u2(t) = ________
is a particular solution of this differential equation. Use variation of parameters to determine u1 (t) and u2 (t).
u1 (t) = ________ u2(t) = ________
(Essay)
4.7/5  (31)
(31)
Which of the following are solutions to the homogeneous second-order differential equation 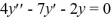 ?
Select all that apply.
?
Select all that apply.
(Multiple Choice)
4.9/5  (25)
(25)
What is the general solution of the homogeneous second-order Cauchy Euler differential equation 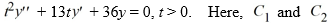 are arbitrary real constants.
are arbitrary real constants.
(Multiple Choice)
4.9/5  (34)
(34)
Consider this second-order nonhomogeneous differential equation:
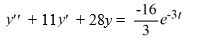 Which of these is a suitable form of a particular solution Y(t) of the nonhomogeneous differential equation if the method of undetermined coefficients is to be used? Here, all capital letters represent arbitrary real constants.
Which of these is a suitable form of a particular solution Y(t) of the nonhomogeneous differential equation if the method of undetermined coefficients is to be used? Here, all capital letters represent arbitrary real constants.
(Multiple Choice)
4.8/5  (30)
(30)
Consider this second-order nonhomogeneous differential equation:
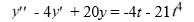 Which of the following is the form of the solution of the corresponding homogeneous differential equation? Here, C1 and C2 are arbitrary real constants.
Which of the following is the form of the solution of the corresponding homogeneous differential equation? Here, C1 and C2 are arbitrary real constants.
(Multiple Choice)
4.8/5  (35)
(35)
Suppose a 96-lb object stretches a spring 3 feet while in equilibrium, and a dashpot provides a damping force of 5 lbs for every foot per second of velocity. The form of the equation of unforced motion of the object in such a spring-mass system is 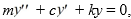 where m is the mass of the object, c is the damping constant, and k is the spring constant. Assume that the spring starts at a height of 3/2 feet below the horizontal with an upward velocity of - 2 feet per second.
For what values of A, B, C, and D can the solution,
where m is the mass of the object, c is the damping constant, and k is the spring constant. Assume that the spring starts at a height of 3/2 feet below the horizontal with an upward velocity of - 2 feet per second.
For what values of A, B, C, and D can the solution, 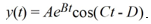 be expressed in the form . Provide the exact values, not decimal approximations.
A = ____________, B = ____________, C = ____________, tan D = ____________
be expressed in the form . Provide the exact values, not decimal approximations.
A = ____________, B = ____________, C = ____________, tan D = ____________
(Essay)
4.8/5  (40)
(40)
For which of these differential equations is the characteristic equation given by r(10r + 1) = 0?
(Multiple Choice)
4.8/5  (40)
(40)
Which of these is the general solution of the second-order nonhomogeneous differential equation 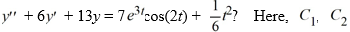 and all capital letters are arbitrary real constants.
and all capital letters are arbitrary real constants.
(Multiple Choice)
4.8/5  (32)
(32)
Consider this initial value problem:
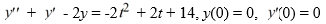 Find a particular solution of the given nonhomogeneous differential equation.
Find a particular solution of the given nonhomogeneous differential equation.
(Essay)
4.8/5  (37)
(37)
Suppose a 10-lb object stretches a spring 2.5 feet while in equilibrium. If the object is displaced an additional 0.5 inches and is then set in motion with an initial upward velocity of -0.7 feet per second.What is the amplitude, R, in feet? Round your answer to the nearest hundredth of a foot.
(Short Answer)
4.9/5  (30)
(30)
Consider this initial value problem:
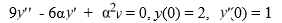 For what values of does the solution tend to 0 as t ?
For what values of does the solution tend to 0 as t ?
(Multiple Choice)
4.8/5  (35)
(35)
Suppose a 160-lb object stretches a spring 12 feet while in equilibrium, and a dashpot provides a damping force of 5 lbs for every foot per second of velocity. The form of the equation of unforced motion of the object in such a spring-mass system is 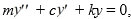 where m is the mass of the object, c is the damping constant, and k is the spring constant. Assume that the spring starts at a height of 1/2 feet below the horizontal with an upward velocity of - 3/2 feet per second.
What is the quasi-frequency? Provide the exact values, not a decimal approximation.
where m is the mass of the object, c is the damping constant, and k is the spring constant. Assume that the spring starts at a height of 1/2 feet below the horizontal with an upward velocity of - 3/2 feet per second.
What is the quasi-frequency? Provide the exact values, not a decimal approximation.
(Short Answer)
4.8/5  (43)
(43)
Which of the following is the general solution of the homogeneous second-order differential equation 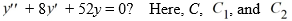 are arbitrary real constants.
are arbitrary real constants.
(Multiple Choice)
5.0/5  (38)
(38)
Suppose a 128-lb object stretches a spring 3 feet while in equilibrium, and a dashpot provides a damping force of 5 lbs for every foot per second of velocity. The form of the equation of unforced motion of the object in such a spring-mass system is 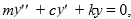 where m is the mass of the object, c is the damping constant, and k is the spring constant. Assume that the spring starts at a height of 5/2 feet below the horizontal with an upward velocity of - 3 feet per second.
For what values of the arbitrary constants C1 and C2 does a general solution of the form y(t) =
where m is the mass of the object, c is the damping constant, and k is the spring constant. Assume that the spring starts at a height of 5/2 feet below the horizontal with an upward velocity of - 3 feet per second.
For what values of the arbitrary constants C1 and C2 does a general solution of the form y(t) = 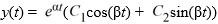 satisfy the initial conditions? Provide the exact values, not decimal approximations.
C1__________, C2____________
satisfy the initial conditions? Provide the exact values, not decimal approximations.
C1__________, C2____________
(Short Answer)
4.9/5  (33)
(33)
Showing 1 - 20 of 119
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)