Exam 3: Quadratic Functions

If $p(t)=-4(t-2)(t+1)$ is quadratic, then it can be written as $p(t)=\ldots t^{2}+\ldots t+\ldots$ . If $p(t)$ is not quadratic, enter "DNE" for each of the blanks.

Suppose $g(x)=4 x^{2}-6 x$ . What is $\frac{g(x+h)-g(x)}{h}$ ?

Find the zeros of $y=10 x^{2}+15 x+5$ . List the answers in the form "A, B", with $\mathrm{A}<\mathrm{B}$ .

Find the zeros of $y=x-5 \sqrt{x}+6$

Find a formula for the quadratic function whose graph has axis of symmetry $x=3.5$ , $y$ - intercept at $y=6$ , and contains the point $(1,-12)$ .

Suppose a farmer has 160 feet of fence and he wants to enclose a pasture with a rectangular boundary. There is already fencing along one side of the field that he wants to enclose, so he will only need to fence 3 sides of the new field. What is the maximum area that he can fence?

Let $f(x)$ be a quadratic function which has $y$ -intercept -54 and has zeros at $x=-3$ and $x=6$ . Then $f(x)=$ ---------- $x^{2}+$ --------- $x+$ --------------

The height of a baseball in feet $t$ seconds after it has been hit is given by $y=2+35 t-16 t^{2}$ . At what time $t$ does the baseball reach maximum height? Give your answer correct to 3 decimal places.

A projectile's height $h(t)$ above ground is a quadratic function of time $t$ in seconds since launched. Three values of the function are given in the table below. 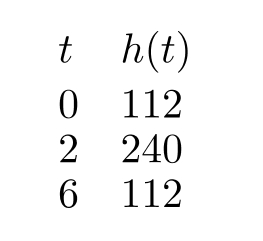What is the practical interpretation of $h(0)$ ?

Let $y=3 x^{2}-18 x+25$ . a) Graph the function. b) Give the vertex. c) Give the axis of symmetry. d) Give the y-intercept.

Find a formula for the quadratic function which has only one zero at $x=3$ and contains the point $(-1,-48)$

Find a formula for the parabola

You want to fence in a rectangular area for a dog run along the back of your home. Your home will serve as one side of the run, so you only need to purchase fencing material for the remaining three sides. The fencing material costs $\$ 1.75$ per foot, and you have a budget of $\$ 49.00$ . How many square feet are in the largest dog run you can afford to build?

What is the equation of the parabola that is concave down, has vertex $(-3,36)$ and contains the origin.

Suppose a quadratic function has vertex $(3,0)$ and has y-intercept 4 . Its formula can be written $y=a(x-b)^{2}$ , where $a=$ ------- and $b=$ ----------

Find a quadratic equation, $f$ , with zeros at $x=4$ and $x=-2$ such that $f(1)=18$ .

The height of a baseball in feet $t$ seconds after it has been hit is given by $y=2+35 t-16 t^{2}$ . What is the maximum height of the baseball? Give your answer correct to 3 decimal places.

Which of the following parabolas have a vertex of $(5,-6)$ ?

Is the function $h(t)=2(x-1)^{2}-6 x$ quadratic? If so, write the function in the form $h(t)=a x^{2}+b x+c$ .

Find a formula for the parabola: