Exam 7: Symmetrical Components

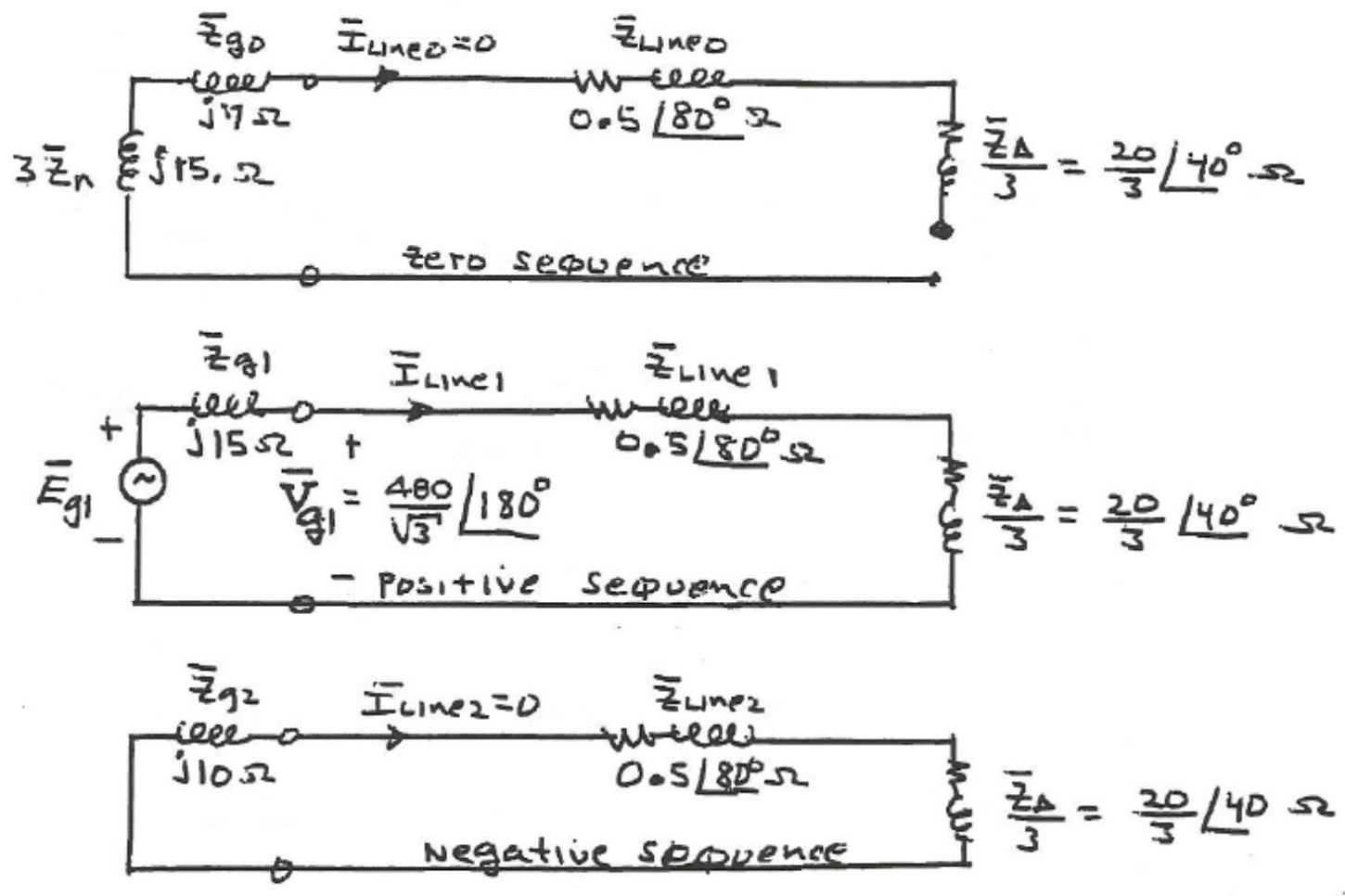
A balanced Y-connected generator with terminal voltage $V_{b c}=480 \angle 90^{\circ}$ volts is connected to a balanced- $\Delta$ load whose impedance is $20 \angle 40^{\circ}$ ohms per phase. The line impedance between the source and load is $0.5 \angle 80^{\circ}$ ohm for each phase. The generator neutral is grounded through an impedance of $j 5 \mathrm{ohms}$ . The generator sequence impedances are given by $Z_{g 0}=j 7, Z_{g 1}=j 15$ , and $Z_{g 2}=j 10 \mathrm{ohms}$ . Draw the sequence networks for this system and determine the sequence components of the line currents.

Free

(Essay)

4.9/5

(42)

Question 1

Correct Answer:

Verified

$\begin{aligned} \bar{I}_{\text {Line } 0} & =\bar{I}_{\text {Line } 2}=0 \\ \bar{I}_{\text {Line } 1} & =\frac{V_{g 1}}{\bar{Ƶ}_{\text {Line } 1}+\frac{\bar{Ƶ}_{\Delta}}{3}}=\frac{\frac{480}{\sqrt{3}} \angle 180^{\circ}}{0.5 \angle 80^{\circ}+\frac{20}{3} \angle 40^{\circ}} \\ & =\frac{277.14 \angle 180^{\circ}}{5.194+j 4.778}=\frac{277.14 \angle 180^{\circ}}{7.057 \angle 42.61^{\circ}}=39.27 \angle 137.4^{\circ} \mathrm{A} \end{aligned}$
$\begin{aligned}\bar{I}_{\text {Line } 0} & =\bar{I}_{\text {Line } 2}=0 \\\bar{I}_{\text {Line } 1} & =\frac{V_{g 1}}{\bar{Ƶ}_{\text {Line } 1}+\frac{\bar{Ƶ}_{\Delta}}{3}}=\frac{\frac{480}{\sqrt{3}} \angle 180^{\circ}}{0.5 \angle 80^{\circ}+\frac{20}{3} \angle 40^{\circ}} \\& =\frac{277.14 \angle 180^{\circ}}{5.194+j 4.778}=\frac{277.14 \angle 180^{\circ}}{7.057 \angle 42.61^{\circ}}=39.27 \angle 137.4^{\circ} \mathrm{A}\end{aligned}$

Find the phase voltages $V_{a n}, V_{b n}$ , and $V_{c n}$ whose sequence components are: $V_{0}=20 \angle 80^{\circ}, V_{1}=100 \angle 0^{\circ}, V_{2}=30 \angle 180^{\circ} \mathrm{V}$ .

Free

(Essay)

4.9/5

(33)

Question 2

Correct Answer:

Verified

$\begin{aligned}{\left[\begin{array}{l}\bar{V}_{a n} \\\bar{V}_{b n} \\\bar{V}_{c n}\end{array}\right] } & =\left[\begin{array}{ccc}1 & 1 & 1 \\1 & a^{2} & a \\1 & a & a^{2}\end{array}\right]\left[\begin{array}{c}20 \angle 80^{\circ} \\100 \angle 0^{\circ} \\30 \angle 180^{\circ}\end{array}\right]=\left[\begin{array}{c}20 \angle 80^{\circ}+100 \angle 0^{\circ}+30 \angle 180^{\circ} \\20 \angle 80^{\circ}+100 \angle 290^{\circ}+30 \angle 300^{\circ} \\20 \angle 80^{\circ}+100 \angle 120^{\circ}+30 \angle 60^{\circ}\end{array}\right] \\& =\left[\begin{array}{c}73.47+j 19.70 \\-31.53-j 92.89 \\-31.53+j 132.3\end{array}\right]=\left[\begin{array}{c}76.07 \angle 15.01^{\circ} \\98.09 \angle 251.3^{\circ} \\135.98 \angle 103.4^{\circ}\end{array}\right] \mathrm{V}\end{aligned}$

Given that the line-to-ground voltages of $V_{a g}=280 \angle 0^{\circ}, V_{b g}=250 \angle-110^{\circ}$ , and $V_{c g}=290 \angle 130^{\circ}$ volts are applied to a balanced-Y load consisting of $(12+j 16)$ ohms per phase. The load neutral is kept open. Draw the sequence networks and calculate $I_{0}, I_{1}$ , and $I_{2}$ , the sequence components of the line currents. Then calculate the line currents $I_{a}, I_{b}$ , and $I_{c}$ .

Free

(Essay)

4.8/5

(38)

Question 3

Correct Answer:

Verified

$\bar{I}_{0}=0 From Test Bank Problem 8.5, \bar{I}_{1}=27.57 \angle-59.76^{\circ} \mathrm{A} ; \bar{I}_{2}=2.487 \angle 26.3^{\circ} \mathrm{A} \begin{aligned} {\left[\begin{array}{c} \bar{I}_{a} \\ \bar{I}_{b} \\ \bar{I}_{c} \end{array}\right] } & =\left[\begin{array}{ccc} 1 & 1 & 1 \\ 1 & a^{2} & a \\ 1 & a & a^{2} \end{array}\right]\left[\begin{array}{c} 0 \\ 27.57 \angle-59.76^{\circ} \\ 2.487 \angle 26.3^{\circ} \end{array}\right] \\ & =\left[\begin{array}{c} 27.57 \angle-59.76^{\circ}+2.487 \angle 26.3^{\circ} \\ 27.57 \angle 180.24^{\circ}+2.487 \angle 146.3^{\circ} \\ 27.57 \angle 60.24^{\circ}+2.487 \angle 266.3^{\circ} \end{array}\right] \\ & =\left[\begin{array}{c} 16.120-j 22.72 \\ -29.64+j 1.2650 \\ 13.530+j 21.46 \end{array}\right]=\left[\begin{array}{l} 27.86 \angle-54.64^{\circ} \\ 29.66 \angle 177.56^{\circ} \\ 25.36 \angle 57.77^{\circ} \end{array}\right] \mathrm{A} \end{aligned}$
$\bar{I}_{0}=0$
From Test Bank Problem 8.5, $\bar{I}_{1}=27.57 \angle-59.76^{\circ} \mathrm{A} ; \bar{I}_{2}=2.487 \angle 26.3^{\circ} \mathrm{A}$
$\begin{aligned}{\left[\begin{array}{c}\bar{I}_{a} \\\bar{I}_{b} \\\bar{I}_{c}\end{array}\right] } & =\left[\begin{array}{ccc}1 & 1 & 1 \\1 & a^{2} & a \\1 & a & a^{2}\end{array}\right]\left[\begin{array}{c}0 \\27.57 \angle-59.76^{\circ} \\2.487 \angle 26.3^{\circ}\end{array}\right] \\& =\left[\begin{array}{c}27.57 \angle-59.76^{\circ}+2.487 \angle 26.3^{\circ} \\27.57 \angle 180.24^{\circ}+2.487 \angle 146.3^{\circ} \\27.57 \angle 60.24^{\circ}+2.487 \angle 266.3^{\circ}\end{array}\right] \\& =\left[\begin{array}{c}16.120-j 22.72 \\-29.64+j 1.2650 \\13.530+j 21.46\end{array}\right]=\left[\begin{array}{l}27.86 \angle-54.64^{\circ} \\29.66 \angle 177.56^{\circ} \\25.36 \angle 57.77^{\circ}\end{array}\right] \mathrm{A}\end{aligned}$

Given that line-to-ground voltages of $V_{a g}=280 \angle 0^{\circ}, V_{b g}=250 \angle-110^{\circ}$ , and $V_{c g}=290 \angle 130^{\circ}$ volts are applied to a balanced- $\Delta$ load consisting of $(12+j 16)$ ohms per phase. The load neutral is solidly grounded. Draw the sequence networks and calculate $I_{0}$ , $I_{1}$ , and $I_{2}$ , the sequence components of the line currents. Then calculate the line currents $I_{a}, I_{b}$ , and $I_{c}$ .

(Essay)

4.9/5

(33)

Question 4

Given the line-to-ground voltages $V_{a g}=280 \angle 0^{\circ}, V_{b g}=290 \angle-130^{\circ}$ , and $V_{c g}=260 \angle 110^{\circ}$ volts, calculate (a) the sequence components of the line-to-ground voltages, denoted $V_{\mathrm{L} g 0}, V_{\mathrm{L} g 1}$ , and $V_{\mathrm{L} g 2}$ ; (b) line-to-line voltages $V_{a b}, V_{b c}$ , and $V_{c a}$ ; and (c) sequence components of the line-to-line voltages $V_{\mathrm{LL} 0}, V_{\mathrm{LL} 1}$ , and $V_{\mathrm{LL} 2}$ . Also, verify the following general relation: $V_{\mathrm{LL} 0}=0, V_{\mathrm{LL} 1}=\sqrt{3} V_{\mathrm{L} g 1} \angle+30^{\circ}$ , and $V_{\mathrm{LL} 2}=\sqrt{3} V_{\mathrm{L} g 2} \angle-30^{\circ}$ volts.

(Essay)

4.8/5

(36)

Question 5

The currents in a $\Delta$ load are $I_{a b}=10 \angle 0^{\circ}, I_{b c}=20 \angle-90^{\circ}$ , and $I_{c a}=15 \angle 90^{\circ}$ A. Calculate (a) the sequence components of the $\Delta$ -load currents, denoted $I_{\Delta 0}, I_{\Delta 1}, I_{\Delta 2}$ ; (b) the line currents $I_{a}, I_{b}$ , and $I_{c}$ , which feed the $\Delta$ load; and (c) sequence components of the line currents $I_{\mathrm{L} 0}, I_{\mathrm{L} 1}$ , and $I_{\mathrm{L} 2}$ . Also, verify the following general relation: $I_{\mathrm{L} 0}=0$ , $I_{\mathrm{L} 1}=\sqrt{3} I_{\Delta 1} \angle-30^{\circ}$ , and $I_{\mathrm{L} 2}=\sqrt{3} I_{\Delta 2} \angle+30^{\circ} \mathrm{A}$ .

(Essay)

4.8/5

(41)

Question 6

In a three-phase system, a synchronous generator supplies power to a 208-volt synchronous motor through a line having an impedance of $0.5 \angle 80^{\circ}$ ohm per phase. The motor draws $10 \mathrm{~kW}$ at 0.8 p.f. leading and at rated voltage. The neutrals of both the generator and motor are grounded through impedances of $j 5 \mathrm{ohms}$ . The sequence impedances of both machines are $Z_{0}=j 5, Z_{1}=j 15$ , and $Z_{2}=j 10$ ohms. Draw the sequence networks for this system and find the line-to-line voltage at the generator terminals. Assume balanced three-phase operation.

(Essay)

4.9/5

(37)

Question 7

Given that line-to-ground voltages of $V_{a g}=280 \angle 0^{\circ}, V_{b g}=250 \angle-110^{\circ}$ , and $V_{c g}=290 \angle 130^{\circ}$ volts are applied to a balanced-Y load consisting of $(3+j 4)$ ohms per phase between the source and the load. The load neutral is solidly grounded. Draw the sequence networks and calculate $I_{0}, I_{1}$ , and $I_{2}$ , the sequence components of the line currents. Then calculate the line currents $I_{a}, I_{b}$ , and $I_{c}$ .

(Essay)

4.7/5

(26)

Question 8

One line of a three-phase generator is open circuited, while the other two are short-circuited to ground. The line currents are $I_{a}=0, I_{b}=1500 / 90^{\circ}$ , and $I_{c}=$ $1500 \angle-30^{\circ}$ A. Find the symmetrical components of these currents. Also find the current into the ground.

(Essay)

4.8/5

(29)

Question 9

Given that line-to-ground voltages of $V_{a g}=280 \angle 0^{\circ}, V_{b g}=250 \angle-110^{\circ}$ , and $V_{c g}=290 \angle 130^{\circ}$ volts are applied to a balanced-Y load consisting of $(3+j 4)$ ohms per phase between the source and the load. The load neutral is solidly grounded. Draw the sequence networks and calculate $I_{0}, I_{1}$ , and $I_{2}$ , the sequence components of the line currents. Then calculate the line currents $I_{a}, I_{b}$ , and $I_{c}$ . Also calculate the real and reactive power delivered to the three-phase load.

(Essay)

4.9/5

(41)

Question 10

Determine the symmetrical components of the following line currents: (a) $I_{a}=10 \angle 90^{\circ}$ , $I_{b}=10 \angle 340^{\circ}, I_{c}=10 \angle 200^{\circ} \mathrm{A}$ ; (b) $I_{a}=100, I_{b}=j 100, I_{c}=0 \mathrm{~A}$ .

(Essay)

4.9/5

(27)

Question 11

Using the operator $a=1 \angle 120^{\circ}$ , evaluate the following in polar form: (a) $(a+1) /$ $\left(1+a-a^{2}\right)$ , (b) $\left(a^{2}+a+j\right) /\left(j a-a^{2}\right),\left(\right.$ c) $(1-a)\left(1+a^{2}\right)$ , (d) $\left(a+a^{2}\right)\left(a^{2}+1\right)$ .

(Essay)

4.8/5

(31)

Question 12

Find the phase voltages $V_{a n}, V_{b n}$ , and $V_{c n}$ whose sequence components are: $V_{0}=20 \angle 80^{\circ}, V_{1}=100 \angle 0^{\circ}, V_{2}=30 \angle 180^{\circ} \mathrm{V}$ .

One line of a three-phase generator is open circuited, while the other two are short-circuited to ground. The line currents are $I_{a}=0, I_{b}=1500 / 90^{\circ}$ , and $I_{c}=$ $1500 \angle-30^{\circ}$ A. Find the symmetrical components of these currents. Also find the current into the ground.

Determine the symmetrical components of the following line currents: (a) $I_{a}=10 \angle 90^{\circ}$ , $I_{b}=10 \angle 340^{\circ}, I_{c}=10 \angle 200^{\circ} \mathrm{A}$ ; (b) $I_{a}=100, I_{b}=j 100, I_{c}=0 \mathrm{~A}$ .

Using the operator $a=1 \angle 120^{\circ}$ , evaluate the following in polar form: (a) $(a+1) /$ $\left(1+a-a^{2}\right)$ , (b) $\left(a^{2}+a+j\right) /\left(j a-a^{2}\right),\left(\right.$ c) $(1-a)\left(1+a^{2}\right)$ , (d) $\left(a+a^{2}\right)\left(a^{2}+1\right)$ .

Fundamentals

Power Transformers

Transmission Line Parameters

Transmission Lines: Steady-State Operation

Power Flows

Symmetrical Faults

Filters