Exam 29: Applied Applications of the Derivative
Exam 1: Numerical Computation129 Questions
Exam 2: Introduction to Algebra130 Questions
Exam 3: Simple Equations and Word Problems83 Questions
Exam 4: Functions85 Questions
Exam 5: Graphs64 Questions
Exam 6: Geometry103 Questions
Exam 7: Right Triangles and Vectors88 Questions
Exam 8: Factors and Factoring136 Questions
Exam 9: Fractions and Fractional Equations155 Questions
Exam 10: Systems of Linear Equations75 Questions
Exam 11: Determinants75 Questions
Exam 12: Matrices96 Questions
Exam 13: Exponents and Radicals125 Questions
Exam 14: Quadratic Equations151 Questions
Exam 15: Oblique Triangles and Vectors89 Questions
Exam 16: Radian Measure, Arc Length, and Circular Motion75 Questions
Exam 17: Graphs of the Trigonometric Functions70 Questions
Exam 18: Trigonometric Identities and Equations116 Questions
Exam 19: Ratio, Proportion, and Variation98 Questions
Exam 20: Exponential and Logarithmic Functions140 Questions
Exam 21: Complex Numbers115 Questions
Exam 22: Analytic Geometry129 Questions
Exam 23: Binary, Hexadecimal, Octal, and Bcd Numbers110 Questions
Exam 24: Inequalities and Linear Programming39 Questions
Exam 25: Sequences, Series, and the Binomial Theorem121 Questions
Exam 26: Introduction to Statistics and Probability68 Questions
Exam 27: Derivatives of Algebraic Functions83 Questions
Exam 28: Graphical Applications of the Derivative50 Questions
Exam 29: Applied Applications of the Derivative71 Questions
Exam 30: Integration69 Questions
Exam 31: Applications of the Integral50 Questions
Exam 32: More Applications of the Integral58 Questions
Exam 33: Derivatives of Trigonometric, Logarithmic, and Exponential Functions113 Questions
Exam 34: Methods of Integration89 Questions
Exam 35: Differential Equations103 Questions
Exam 36: Solving Differential Equations by the Laplace Transform and by Numerical Methods56 Questions
Exam 37: Infinite Series60 Questions
Select questions type
A car is on a road traveling due north at and a motorcycle is traveling on another road due west at . The car is from the point where the roads meet and the motorcycle is past that point. What is the closest that the two vehicles get?
(Short Answer)
4.8/5  (35)
(35)
The tent is in the shape of a triangular prism, with both ends covered, but with no bottom. It has a rectangular base with a width that is half its length. The tent must have a volume of . Find the width of the tent that minimizes the surface area of the tent.
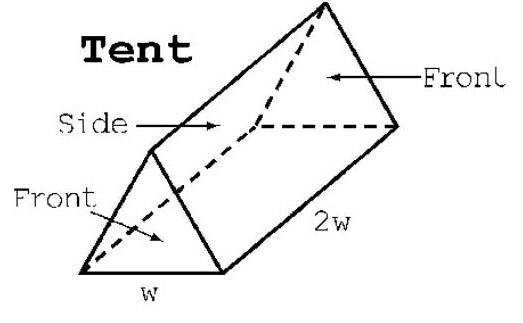
(Short Answer)
4.7/5  (38)
(38)
A point moves according to the equation , where is in centimetres and is in seconds.
(a) Find the time in seconds greater than zero when the point comes to rest and the distance it traveled in this time.
(b) Find the non-zero time when the point crosses its starting point.
(Short Answer)
4.9/5  (26)
(26)
Find the area of the largest rectangle with sides parallel to the coordinate axes which can be inscribed in the figure bounded by the parabolas and .
(Short Answer)
4.8/5  (31)
(31)
A boat with an anchor on the bottom at a depth of is drifting away from the anchor at , while the anchor cable slips out at water level. At what rate is the cable leaving the boat when the boat has drifted away from the spot directly above the anchor? Assume that the cable is straight.
(Short Answer)
4.9/5  (39)
(39)
The cost of manufacturing a crankshaft per hour follows the equation where is the number of crankshafts. What is the optimum number of crankshafts to minimize production costs?
(Short Answer)
4.9/5  (46)
(46)
A ladder is leaning against the side of a building. At what rate is the top of the ladder sliding down the building if the bottom of the ladder is from the base of the building and being pulled away from the building at ?
(Short Answer)
4.8/5  (33)
(33)
The air in a container is at a pressure of when its volume is . Find the rate of change of the volume with respect to pressure as the pressure increases. Use Boyles' Law, .
(Short Answer)
4.7/5  (35)
(35)
What is the minimum amount of metal needed to make a cylindrical drum? Express our answer to the nearest whole square centimetre.
(Short Answer)
4.8/5  (35)
(35)
The current in a inductor is given by . Find the voltage across the inductor at .
(Short Answer)
4.8/5  (44)
(44)
The formula for the volume of fluid in a spherical tank of radius when the depth of the fluid is A wide tank is filling with liquid oxygen at a constant rate of . How fast is the surface of the oxygen rising when the height is ?
(Short Answer)
4.7/5  (34)
(34)
Showing 61 - 71 of 71
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)