Exam 12: Hypothesis Testing for Two Populations

A product researcher wants to determine if there is a difference in the rate at which men and women become proficient at using a new software package. A study of 51 men and 46 women produced the following results: 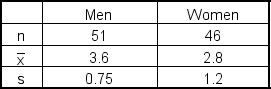At α = 0.05, is there evidence of a statistically significant difference between the time it takes men to become proficient at this particular software compared to the time it takes women? Assume equal population variances.

You are evaluating investing in a cognitive training company. For this reason, you want to determine whether users who complete at least 75% of the recommended daily training for two months show improved levels of reading comprehension and problem solving skills. You select a random sample of new users and get test scores for each participant in the sample. The test score is a composite of reading comprehension and problem solving skills. Two months later, you randomly select 15 users who have completed 75% or more of the recommended training for the last two months and have them take a test similar to the initial test. You are interested in determining whether the average test score before training is different than the average test score after training for this sample. The after-training average is 92.8, which is 2.7 points higher than the before-training average. The sample standard deviations of the differences is 1.2. You can assume that the differences are normally distributed in the population. The observed t value for this test is ___.

Your company is evaluating two cloud-based secured data storage services. "Pie in the Sky," the newer service, claims its uploading and downloading speeds are faster than the older service, "Cloudy but Steady Skies." You need to make a decision based on published access times for both services at different times and for varying file sizes. To make your decision, you purchase a statistical study, which indicates that average download time for Pie in the Sky is 0.77 sec. per MB and for Cloudy but Steady Skies is 0.84. Assume that n₁ = n₂ = 50, $\sigma$ ₁ = 0.2 and $\sigma$ ₂ = 0.3. With $\alpha$ =.05, the appropriate decision is ___.

A researcher is estimating the average difference between two population means based on matched?pairs samples. She gathers data on each pair in the study resulting in: 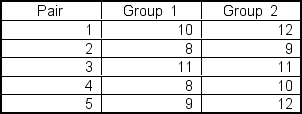Assume that the data are normally distributed in the population. To obtain a 95% confidence interval, the table t value would be ___.

A researcher wishes to determine the difference in two population means. To do this, she randomly samples 9 items from each population and computes a 90% confidence interval. The sample from the first population produces a mean of 780 with a standard deviation of 240. The sample from the second population produces a mean of 890 with a standard deviation of 280. Assume that the values are normally distributed in each population. The point estimate for the difference in the means of these two populations is ___.

Lucy Baker is analyzing demographic characteristics of two television programs, American Idol (population 1) and 60 Minutes (population 2). Previous studies indicate no difference in the ages of the two audiences. (The mean age of each audience is the same.) Lucy plans to test this hypothesis using a random sample of 100 from each audience. Her alternate hypothesis is ___.

A researcher wishes to determine the difference in two population means. To do this, she randomly samples 9 items from each population and computes a 90% confidence interval. The sample from the first population produces a mean of 780 with a standard deviation of 240. The sample from the second population produces a mean of 890 with a standard deviation of 280. Assume that the values are normally distributed in each population and that the population variances are approximately equal. The critical t value used from the table for this is ___.

A researcher is interested in testing to determine if the mean price of a casual lunch is different in the city than it is in the suburbs. The null hypothesis is that there is no difference in the population means (i.e., the difference is zero). The alternative hypothesis is that there is a difference (i.e., the difference is $\textbf{ not }$ equal to zero). He randomly selects a sample of 9 lunch tickets from the city population resulting in a mean of $14.30 and a standard deviation of $3.40. He randomly selects a sample of 14 lunch tickets from the suburban population resulting in a mean of $11.80 and a standard deviation $2.90. He is using an alpha value of.10 to conduct this test. Assuming that the populations are normally distributed, the critical t value from the table is ___.

Lucy Baker is analyzing demographic characteristics of two television programs, American Idol (population 1) and 60 Minutes (population 2). Previous studies indicate no difference in the ages of the two audiences. (The mean age of each audience is the same.) Her staff randomly selected 100 people from each audience, and reported the following: 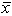₁ = 43 years and 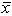₂ = 45 years. Assume that $\sigma$ ₁ = 5 and $\sigma$ ₂ = 8. Assuming a two-tail test and $\alpha$ =.05, the observed z value is ___.

In a set of matched samples, each data value in one sample is related to or matched with a corresponding data value in the other sample.

Suppose that.06 of each of two populations possess a given characteristic. Samples of size 400 are randomly drawn from each population. What is the probability that the differences in sample proportions will be greater than 0.02?

A researcher wants to conduct a before/after study on 11 subjects to determine if a new cholesterol medication results in higher HDL cholesterol readings. The null hypothesis is that the average difference is zero while the alternative hypothesis is that the average difference is $\textbf{ not }$ zero. Scores are obtained on the subjects both before and after taking the medication. After subtracting the after scores from the before scores, the average difference is computed to be -2.40 with a sample standard deviation of 1.21. A 0.05 level of significance is selected. Assume that the differences are normally distributed in the population. The table t value for this test is ___.