Exam 24: Strategic Thinking and Game Theory

If a separating equilibrium is played in a signaling game, the receiver will "update" his beliefs during the game.

If everyone has a dominant strategy in a simultaneous move game, then the action that is played by that strategy is played in all stages of any finitely repeated version of that game in any subgame perfect equilibrium.

The Folk Theorem says that anything can happen in infinitely repeated games.

If a pooling equilibrium is played in a signaling game, the receiver will update her beliefs about the sender before settling on her best option.

A mixed strategy in which positive probability is placed on more than one action can be a best response to another player's strategy only if the expected payoff from playing the pure strategies (over which the individual is mixing) is the same.

Suppose a player can play 2 possible actions and has 5 possible decision nodes in a sequential game.Then he has 10 possible strategies he can play.

Consider the game depicted below.Player 1 decides between going L or R in stage 1 and 3 of the game.Player 2 decides between going l and r in stage 2 of the game. 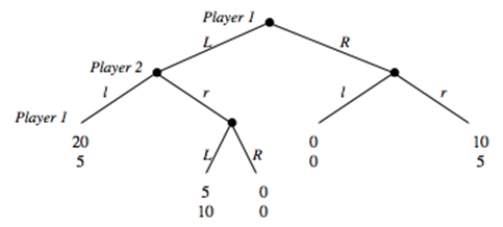a.List the possible pure strategies for each player in this game and illustrate the payoffs from each pair of strategies in a matrix. b.Is there a dominant strategy for either player? c.Identify the subgame perfect equilibrium strategies and outcome. d.Identify the Nash Equilibria that are not subgame perfect. e.For each Nash Equilibrium that is not subgame perfect, explain which parts of the Nash Equilibrium strategies are non-credible.f.Suppose you have developed a drug that can be administered without the victim being aware of it.The effect of the drug is that the victim suddenly becomes gullible and believes anything he is told.You only have 1 dose of the drug and decide to auction it off to the two players right before they play each other in the game you have analyzed so far.Each player is asked to submit a sealed bid, and the highest bidder will be sold the drug at a price equal to the highest bid.In case of a tie in bids, a coin is flipped to determine who wins and pays the price that was bid.Suppose in this part that payoffs are in terms of dollars and that bids can be made in one cent increments.Suppose further that players do not consider bidding above the maximum they are willing to pay.Given that the players know each other's payoffs in the above game, what is the equilibrium price that you will be able to sell the drug for? (Hint: There are two possible answers.) g.In part (f), we said "Suppose further that players do not consider bidding above the maximum they are willing to pay." Can you think of a Nash equilibrium to the auction that would end in a price of $8 if we had not made that statement in (f)?

In a Bayesian incomplete information game, a "belief" is represented as the probability you place on your opponent playing one strategy versus another.

Suppose player 1 potentially moves twice in a sequential game, each time choosing from one of two possible actions -- "Left" or "Right".His first move is at the beginning of the game.He gets to move a second time if he moved "Left" the first time and after observing one of two possible actions by player 2 ("Up" or "Down").But if he moves "Right" in the first stage, he gets no further moves and the game ends after player 2 chooses one of two actions ("Up" or "Down").Draw the game tree and list all possible strategies for players 1 and 2.

Any non-credible threat that is part of a Nash equilibrium in a sequential game cannot be played along the Nash equilibrium path.

Dominant strategy Nash equilibria are efficient.

Every subgame perfect equilibrium is a Nash equilibrium but not every Nash equilibrium is a subgame perfect equilibrium.

If players discount the future sufficiently, cooperation in infinitely repeated Prisoners' Dilemma games cannot emerge as a subgame perfect equilibrium.

A Prisoner's Dilemma game is one in which not cooperating is a dominant strategy despite cooperation making everyone better off.

In a simultaneous move game, the number of possible pure strategies a player can play is equal to the number of actions he can choose to take.

A dominant strategy is one that is prevailing.

Non-credible threats that are made in a Nash equilibrium (that is not subgame perfect) of a sequential game cannot be made in the first stage by the player who begins the game.

Cooperation is difficult to achieve in a Prisoners' Dilemma because each player thinks the other player might not cooperate.

If everyone has a dominant strategy, there can be no mixed strategy equilibrium.

In any subgame perfect equilibrium to an infinitely repeated Prisoners' Dilemma game, the players will end up cooperating.