Exam 24: Strategic Thinking and Game Theory
Exam 1: Introduction12 Questions
Exam 2: A Consumers Economic Circumstances26 Questions
Exam 3: Economic Circumstances in Labor and Financial Markets15 Questions
Exam 4: Tastes and Indifference Curves17 Questions
Exam 5: Different Types of Tastes20 Questions
Exam 6: Doing the Best We Can20 Questions
Exam 7: Income and Substitution Effects in Consumer Goods Markets27 Questions
Exam 8: Wealth and Substitution Effects in Labor and Capital Markets19 Questions
Exam 9: Demand for Goods and Supply of Labor and Capital24 Questions
Exam 10: Consumer Surplus and Deadweight Loss28 Questions
Exam 11: One Input and One Output: a Short-Run Producer Model34 Questions
Exam 12: Production With Multiple Inputs34 Questions
Exam 13: Production Decisions in the Short and Long Run31 Questions
Exam 14: Competitive Market Equilibrium24 Questions
Exam 15: The Invisible Hand and the First Welfare Theorem24 Questions
Exam 16: General Equilibrium25 Questions
Exam 17: Choice and Markets in the Presence of Risk26 Questions
Exam 18: Elasticities, Price-Distorting Policies, and Non-Price Rationing28 Questions
Exam 19: Distortionary Taxes and Subsidies32 Questions
Exam 20: Prices and Distortions Across Markets22 Questions
Exam 21: Externalities in Competitive Markets25 Questions
Exam 22: Asymmetric Information in Competitive Markets24 Questions
Exam 23: Monopoly38 Questions
Exam 24: Strategic Thinking and Game Theory37 Questions
Exam 25: Oligopoly22 Questions
Exam 26: Product Differentiation and Innovation in Markets16 Questions
Exam 27: Public Goods21 Questions
Exam 28: Governments and Politics19 Questions
Exam 29: What Is Good Challenges From Psychology and Philosophy23 Questions
Select questions type
Consider player n in a sequential game.
a.If the player can play 2 actions from a single node, how many pure strategies does he have?
b.Suppose he can play 2 actions at each of two different nodes.How many pure strategies does he have now?
c.Suppose he can play 2 actions at each of three different nodes.How many pure strategies does he have now?
d.Suppose he can play 2 actions at each of four different nodes.How many pure strategies does he have now?
e.Suppose he can play 2 actions at each of k different nodes.How many pure strategies does he have now?
(Essay)
4.8/5  (36)
(36)
If a player's strategy in a sequential game is to choose an action that stops the game early on, it is unnecessary to specify that player's plans for moves later on in the game when it would have been his turn to move again.
(True/False)
4.8/5  (28)
(28)
If a pooling equilibrium is played in a signaling game, beliefs about the sender type can take on any form along the branch of the game tree that is not played in equilibrium, but on the branch that is played, beliefs are identical to the probability distribution with which "nature" assigned types to the sender.
(True/False)
4.7/5  (44)
(44)
Bayesian updating in a separating equilibrium implies the initially uninformed player will fully know what type he is playing when he has to make his move.
(True/False)
4.9/5  (42)
(42)
If there is no pure strategy Nash equilibrium in a complete information game, there is a mixed strategy equilibrium, and if there is no mixed strategy equilibrium, there is a pure strategy equilibrium.
(True/False)
4.8/5  (37)
(37)
Suppose a player in a sequential game has 2 potential decision nodes, with 5 possible actions at each node.Then he has 25 possible pure strategies.
(True/False)
4.9/5  (33)
(33)
A complete information game is a special case of an incomplete information game -- where "Nature" assigns each player a "type" with probability 1.
(True/False)
4.7/5  (39)
(39)
If all players in a game have a dominant strategy, then there can only be one pure strategy Nash equilibrium to the game.
(True/False)
4.8/5  (40)
(40)
In a Prisoners' Dilemma, both players are willing to pay to be forced to cooperate.
(True/False)
4.8/5  (32)
(32)
If we depict a simultaneous move, complete information game in a game tree, each player only has one information set no matter how many players there are in the game.
(True/False)
4.7/5  (37)
(37)
In simultaneous move Bayesian games, a player's beliefs are fully given by the probability distribution used by "Nature" to assign types.
(True/False)
4.8/5  (38)
(38)
Consider the following sequential move game: 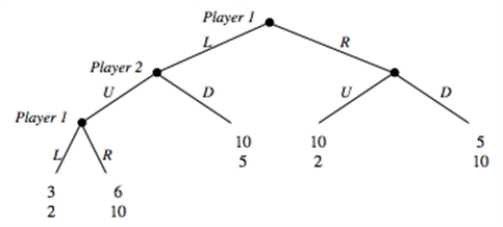 a.What are the subgame perfect equilibrium strategies in this game?
b.List all possible strategies for the two players.
c.Illustrate this game in a payoff matrix.
d.Indicate the Nash equilibria in the payoff matrix from (c).
e.What makes some of the Nash equilibria not subgame perfect?
a.What are the subgame perfect equilibrium strategies in this game?
b.List all possible strategies for the two players.
c.Illustrate this game in a payoff matrix.
d.Indicate the Nash equilibria in the payoff matrix from (c).
e.What makes some of the Nash equilibria not subgame perfect?
(Essay)
4.9/5  (44)
(44)
In mixed strategy Nash equilibria, players play each of two pure strategies with probability 0.5.
(True/False)
5.0/5  (36)
(36)
In a simultaneous move, incomplete information game in which player 1 is unsure of which of two types player 2 is, player 1's strategy must include an action for each possible type that player 2 might be, but player 2 only needs to pick one action since he knows what type he is.
(True/False)
4.8/5  (27)
(27)
Consider player n in a sequential game.
a.If the player can play 3 actions from a single node, how many pure strategies does he have?
b.Suppose he can play 3 actions at each of two different nodes.How many pure strategies does he have now?
c.Suppose he can play 3 actions at each of three different nodes.How many pure strategies does he have now?
d.Suppose he can play 3 actions at each of four different nodes.How many pure strategies does he have now?
e.Suppose he can play 3 actions at each of k different nodes.How many pure strategies does he have now?
(Essay)
4.8/5  (29)
(29)
Complete information sequential games can be represented in payoff matrices and complete information simultaneous games can be represented in game trees with information sets.
(True/False)
4.8/5  (39)
(39)
Suppose a player in a sequential game has 5 potential decision nodes, with 2 possible actions at each node.Then he has 25 possible pure strategies.
(True/False)
4.9/5  (36)
(36)
Showing 21 - 37 of 37
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)