Exam 4: Demand Relationships Among Goods
Exam 1: Preferences and Utility14 Questions
Exam 2: Utility Maximization and Choice15 Questions
Exam 3: Income and Substitution Effects22 Questions
Exam 4: Demand Relationships Among Goods18 Questions
Exam 5: Uncertainty19 Questions
Exam 6: Game Theory20 Questions
Exam 7: Production Functions14 Questions
Exam 8: Cost Functions20 Questions
Exam 9: Profit Maximization32 Questions
Exam 10: The Partial Equilibrium Competitive Model32 Questions
Exam 11: General Equilibrium and Welfare24 Questions
Exam 12: Monopoly22 Questions
Exam 13: Imperfect Competition21 Questions
Exam 14: Labor Markets20 Questions
Exam 15: Capital and Time20 Questions
Exam 16: Asymmetric Information18 Questions
Exam 17: Externalities and Public Goods25 Questions
Select questions type
With only two goods,x and y,if x and y are gross substitutes,a rise in px must necessarily:
Free
(Multiple Choice)
4.8/5  (34)
(34)
Correct Answer:
C
Use the following definitions for an individual who consumes only two goods,x and y:
sx = share of income spent on x.
sy = 1-sx. 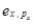 = price elasticity of demand for x.
= price elasticity of demand for x. 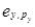 = price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y.
= price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y. 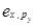 = cross price elasticity of demand for x.
= cross price elasticity of demand for x. 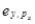 = cross price elasticity of demand for y.
-If the demand for x is given by
= cross price elasticity of demand for y.
-If the demand for x is given by 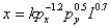 ,which of parameter values hold?
,which of parameter values hold?
Free
(Multiple Choice)
5.0/5  (31)
(31)
Correct Answer:
B
In the Slutsky equation for 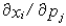 ,the income effect is given by:
,the income effect is given by:
Free
(Multiple Choice)
4.7/5  (31)
(31)
Correct Answer:
B
Quasi-concavity of utility functions insures that with only two goods,these goods must be:
(Multiple Choice)
4.9/5  (23)
(23)
If goods x and y are complements,then the cross price elasticity of demand between them will be:
(Multiple Choice)
4.7/5  (37)
(37)
The attributes model of consumer choice explains the possibility that an individual does not purchase a particular good,z by assuming:
(Multiple Choice)
4.9/5  (31)
(31)
Use the following definitions for an individual who consumes only two goods,x and y:
sx = share of income spent on x.
sy = 1-sx. 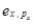 = price elasticity of demand for x.
= price elasticity of demand for x. 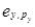 = price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y.
= price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y. 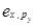 = cross price elasticity of demand for x.
= cross price elasticity of demand for x. 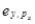 = cross price elasticity of demand for y.
-Homogeneity of the demand function is shown by:
= cross price elasticity of demand for y.
-Homogeneity of the demand function is shown by:
(Multiple Choice)
4.7/5  (43)
(43)
Use the following definitions for an individual who consumes only two goods,x and y:
sx = share of income spent on x.
sy = 1-sx. 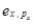 = price elasticity of demand for x.
= price elasticity of demand for x. 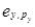 = price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y.
= price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y. 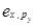 = cross price elasticity of demand for x.
= cross price elasticity of demand for x. 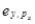 = cross price elasticity of demand for y.
-The elasticity of the compensated demand curve
= cross price elasticity of demand for y.
-The elasticity of the compensated demand curve 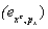 Can be computed as:
Can be computed as:
(Multiple Choice)
4.7/5  (31)
(31)
Use the following definitions for an individual who consumes only two goods,x and y:
sx = share of income spent on x.
sy = 1-sx. 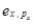 = price elasticity of demand for x.
= price elasticity of demand for x. 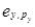 = price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y.
= price elasticity of demand for y.
ex,I = income elasticity of demand for x.
ey,I = income elasticity of demand for y. 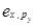 = cross price elasticity of demand for x.
= cross price elasticity of demand for x. 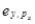 = cross price elasticity of demand for y.
-A generalization of Engel's Law is given by:
= cross price elasticity of demand for y.
-A generalization of Engel's Law is given by:
(Multiple Choice)
4.7/5  (35)
(35)
For the Cobb-Douglas utility function with two goods,the sum of the own price elasticities of demand must be:
(Multiple Choice)
4.9/5  (40)
(40)
"Hicks' Third Law of Demand" states that "most" goods must be:
(Multiple Choice)
4.8/5  (25)
(25)
Two goods are Hicks (net)substitutes if a rise in the price of one causes a(n):
(Multiple Choice)
4.9/5  (37)
(37)
For the "Composite Commodity Theorem" to hold,all goods in the composite must:
(Multiple Choice)
4.8/5  (39)
(39)
The primary additional insight provided by expanding the theory of demand from two to three goods is that a pair of goods may now be:
(Multiple Choice)
4.8/5  (38)
(38)
Symmetry of net substitution effects is one of the principal conclusions of the theory of utility maximization.Which two mathematical theorems are used to prove this symmetry?
(Multiple Choice)
4.7/5  (37)
(37)
If utility is separable in a three-good utility function x3
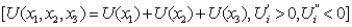 Then for changes in
Then for changes in  Must:
Must:
(Multiple Choice)
4.8/5  (38)
(38)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)