Exam 11: Uncertainty

Gaston Gourmand loves good food. Due to an unusual ailment, he has a probability of 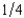of losing his sense of smell, which would greatly reduce his enjoyment of food. Gaston finds an insurance company that will sell him insurance where Gaston gets $3x if he loses his smell and pays $x if he doesn't. He can also buy negative insurance, where Gaston pays $3x if he loses his sense of smell and gets $x if he doesn't. Gaston says, "Money will be only half as important to me if I lose my sense of smell." If we look at his expected utility function, we see what he means. Where c₁ is his consumption if he retains his sense of smell and c₂ is his income if he loses his sense of smell, Gaston has the expected utility function U(c₁, c₂) = 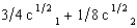. What insurance should he buy?

Gary likes to gamble. Donna offers to bet him $70 on the outcome of a boat race. If Gary's boat wins, Donna would give him $70. If Gary's boat does not win, Gary would give her $70. Gary's utility function is U(c₁, c₂, p₁, p₂) = p₁c²₁ + p₂c²₁, where p₁ and p₂ are the probabilities of events 1 and 2 and where c₁ and c₂ are his consumption if events 1 and 2 occur respectively. Gary's total wealth is currently only $80 and he believes that the probability that he will win the race is .3.

Every $1 invested in Safe Sox will yield $2 for sure. Each $1 invested in Wobbly Umbrellas will yield $8 with probability 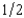and $0 with probability 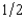. An investor has $10,000 to invest in these two companies and her von Neumann-Morgenstern utility function is the expected value of the natural logarithm of the total yield on her investments. If S is the amount of money that she invests in Safe Sox and $10,000 2 S is the amount that she invests in Wobbly Umbrellas, what should S be to maximize her expected utility? (Pick the closest answer.)

Tom Cruiser's car is worth $100,000. But Tom is careless and leaves the top down and the keys in the ignition. Consequently his car will be stolen with probability .5. If it is stolen, he will never get it back. Tom has $100,000 in other wealth and his von Neumann-Morgenstern utility function for wealth is u(w) = ln(w). Suppose that Tom can buy $K worth of insurance at a price of $.6K. How much insurance will Tom buy?

Timmy Qualm's uncle gave him a lottery ticket. With probability 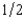the ticket will be worth $100 and with probability 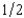it will be worthless. Let x be Timmy's wealth if the lottery ticket is a winner, and y his wealth if it is a loser. Timmy's preferences over alternative contingent commodity bundles are represented by the utility function U(x, y) = min{ 2x - y, 2y - x}. He has no risks other than the ticket.

Buck Columbus is thinking of starting a pinball palace near a large Midwestern university. Buck is an expected utility maximizer with a von Neuman-Morgenstern utility function, U(W) = 1 - ( 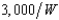), where W is his wealth. Buck's total wealth is $12,000. With probability .2 the palace will be a failure and he'll lose $9,000, so that his wealth will be just $3,000. With probability .8 it will succeed and his wealth will grow to $x. What is the smallest value of x that would be sufficient to make Buck want to invest in the pinball palace rather than have a wealth of $12,000 with certainty?

Billy Pigskin from your workbook has a von Neumann-Morgenstern utility function 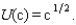If Billy is not injured this season, he will receive an income of $25 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility is

Clancy has $1,200. He plans to bet on a boxing match between Sullivan and Flanagan. For $4, he can buy a coupon that pays $10 if Sullivan wins and nothing otherwise. For $6 he can buy a coupon that will pay $10 if Flanagan wins and nothing otherwise. Clancy doesn't agree with these odds. He thinks that the two fighters each have a probability of 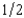of winning. If he is an expected utility maximizer who tries to maximize the expected value of lnW, where lnW is the natural log of his wealth, it would be rational for him to buy

Wilma is not risk averse. She is offered a chance to pay $10 for a lottery ticket that will give her a prize of $100 with probability .06, a prize of $50 with probability .1, and no prize with probability .85. If she understands the odds and makes no mistakes in calculation, she will buy the lottery ticket.

Quincy's expected utility function is pc 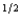₁ + (1 - p)c 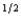₂, where p is the probability that he consumes c₁ and 1 - p is the probability that he consumes c₂. Wilbur is offered a choice between getting a sure payment of $Z or a lottery in which he receives $3,600 with probability .60 and $12,100 with probability .40. Wilbur will choose the sure payment if

Billy Pigskin from your workbook has a von Neumann-Morgenstern utility function 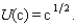If Billy is not injured this season, he will receive an income of $16 million. If he is injured, his income will be only $10,000. The probability that he will be injured is .1 and the probability that he will not be injured is .9. His expected utility is

Willy's only source of wealth is his chocolate factory. He has the utility function pc 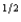_f + (1 - p)c 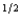_nf, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = 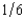. The value of Willy's factory is $500,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company 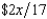whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buy

Willy's only source of wealth is his chocolate factory. He has the utility function pc 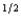_f + (1 - p)c 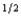_nf, where p is the probability of a flood, 1 - p is the probability of no flood, and c_f and c_nf are his wealth contingent on a flood and on no flood, respectively. The probability of a flood is p = 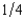. The value of Willy's factory is $300,000 if there is no flood and $0 if there is a flood. Willy can buy insurance where if he buys $x worth of insurance, he must pay the insurance company 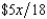whether there is a flood or not but he gets back $x from the company if there is a flood. Willy should buy

Clancy has $1,800. He plans to bet on a boxing match between Sullivan and Flanagan. He finds that he can buy coupons for $9 that will pay off $10 each if Sullivan wins. He also finds in another store some coupons that will pay off $10 if Flanagan wins. The Flanagan tickets cost $1 each. Clancy believes that the two fighters each have a probability of 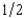of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?

Oliver takes his wealth of $1,000 to a casino. He can bet as much as he likes on the toss of a coin but the "house" takes a cut. If Oliver bets $x on heads, then if heads comes up, he gets $.8x and, if tails comes up, he pays $x. Similarly if he bets $x on tails and if tails comes up, he wins $.8x and, if heads comes up, he pays $x. Draw a graph with dollars contingent on heads and dollars contingent on tails on the two axes. Show Oliver's budget constraint. Oliver is an expected utility maximizer with the utility function 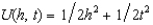, where h is his wealth if heads comes up and t is his wealth if tails comes up. Draw the highest indifference curve that Oliver can reach with his budget. What bets if any does he make?

Harley's current wealth is $600, but there is a .25 probability that he will lose $100. Harley is risk neutral. He has an opportunity to buy insurance that would restore his $100 if he lost it.

Clancy has $5,000. He plans to bet on a boxing match between Sullivan and Flanagan. He finds that he can buy coupons for $5 that will pay off $10 each if Sullivan wins. He also finds in another store some coupons that will pay off $10 if Flanagan wins. The Flanagan tickets cost $5 each. Clancy believes that the two fighters each have a probability of 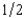of winning. Clancy is a risk averter who tries to maximize the expected value of the natural log of his wealth. Which of the following strategies would maximize his expected utility?

There are two events, 1 and 2. The probability of event 1 is p and the probability of event 2 is 1 - p. Sally Kink is an expected utility maximizer with a utility function is pu(c₁) + (1 - p)u(c₂), where for any number x, u(x) = 2x if x < 1,000 and u(x) = 1,000 + x if x is greater than or equal to 1,000.

Linus Piecewise is an expected utility maximizer. There are two events, H and T, which each have probability 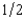. Linus's preferences over lotteries in which his wealth is h if event H happens and t if event T happens are representable by the utility function 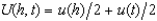. The function u takes the following form. For any x, u(x) = x if x < 100 and u(x) = 100 + 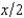if x is greater than or equal to 100. Draw a graph showing the indifference curves for Linus that pass through a. the point (50, 0) b. the point (50, 100) c. the point (100, 100) d. the point (150, 100)