Question 1

In the prisoner's dilemma game, if each prisoner believed that the other prisoner would deny the crime, then both would deny the crime.

Accepted Answer

A) True 
 B)False

Question 2

In a Nash equilibrium, everyone must be playing a dominant strategy.

Accepted Answer

A) True 
 B)False

Question 3

Frank and Nancy met at a sorority sock hop. They agreed to meet for a date at a local bar the next week. Regrettably, they were so fraught with passion that they forgot to agree on which bar would be the site of their rendezvous. Luckily, the town has only two bars, Rizotti's and the Oasis. Having discussed their tastes in bars at the sock hop, both are aware that Frank prefers Rizotti's to the Oasis and Nancy prefer the Oasis to Rizotti's. In fact, the payoffs are as follows. If both go to the Oasis, Nancy's utility is 3 and Frank's utility is 2. If both go to Rizotti's, Frank's utility is 3 and Nancy's utility is 2. If they don't both go to the same bar, both have a utility of 0.

Accepted Answer

A)  This game has no Nash equilibrium in pure strategies. 
B)  This game has a dominant strategy equilibrium. 
C)  There are two Nash equilibrium in pure strategies and a Nash equilibrium in mixed strategies where the probability that Frank and Nancy go to the same bar is. 
D)  This game has two Nash equilibria in pure strategies and a Nash equilibrium in mixed strategies where each person has a probability ofof going to each bar. 
E)  This game has exactly one Nash equilibrium. 
A)  This game has no Nash equilibrium in pure strategies. 
B)  This game has a dominant strategy equilibrium. 
C)  There are two Nash equilibrium in pure strategies and a Nash equilibrium in mixed strategies where the probability that Frank and Nancy go to the same bar is. 
D)  This game has two Nash equilibria in pure strategies and a Nash equilibrium in mixed strategies where each person has a probability ofof going to each bar. 
E)  This game has exactly one Nash equilibrium.

Question 4

Professor Binmore has a monopoly in the market for undergraduate game theory textbooks. The time-discounted value of Professor Binmore's future earnings is $2,000. Professor Ditt is considering writing a book to compete with Professor Binmore's book. With two books amicably splitting the market, the time-discounted value of each professor's future earnings would be $200. If there is full information (each professor knows the profits of the other), under what conditions could Professor Binmore deter the entry of Professor Ditt into his market?

Accepted Answer

A)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would loose $8. In so doing, Professor Binmore would still make $210 over time. 
B)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would only make $8. In so doing, Professor Binmore would still make $100 over time. 
C)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $800. In so doing, Professor Binmore would loose $80 over time. 
D)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $80. In so doing, Professor Binmore would just break even over time. 
E)  None of the above. 
A)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would loose $8. In so doing, Professor Binmore would still make $210 over time. 
B)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would only make $8. In so doing, Professor Binmore would still make $100 over time. 
C)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $800. In so doing, Professor Binmore would loose $80 over time. 
D)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $80. In so doing, Professor Binmore would just break even over time. 
E)  None of the above.

Question 5

Two players are engaged in a game of Chicken. There are two possible strategies, Swerve and Drive Straight. A player who chooses to Swerve is called Chicken and gets a payoff of zero, regardless of what the other player does. A player who chooses to Drive Straight gets a payoff of 36 if the other player swerves and a payoff of -36 if the other player also chooses to Drive Straight. This game has two pure strategy equilibria and

Accepted Answer

A)  a mixed strategy equilibrium in which each player swerves with probability .50 and drives straight with probability .50. 
B)  a mixed strategy equilibrium in which one player swerves with probability .50 and the other swerves with probability .50. 
C)  a mixed strategy in which each player swerves with probability .25 and drives straight with probability .75. 
D)  two mixed strategies in which players alternate between swerving and driving straight. 
E)  no mixed strategies. 
A)  a mixed strategy equilibrium in which each player swerves with probability .50 and drives straight with probability .50. 
B)  a mixed strategy equilibrium in which one player swerves with probability .50 and the other swerves with probability .50. 
C)  a mixed strategy in which each player swerves with probability .25 and drives straight with probability .75. 
D)  two mixed strategies in which players alternate between swerving and driving straight. 
E)  no mixed strategies.

Question 6

In the town of Torrelodones, each of the N > 2 inhabitants has $100. They are told that they can all voluntarily contribute to a fund that will be evenly divided among all residents. If $F are contributed to the fund, the local K-Mart will match the private contributions so that the total amount to be divided is $2F. That is, each resident will get back a payment of $ 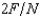  when the fund is divided. If the people in town care only about their own net incomes, in Nash equilibrium, how much will each person contribute to the fund?

Accepted Answer

A)  $0 
B)  $10 
C)  $20 
D)  $50 
E)  $100 
A)  $0 
B)  $10 
C)  $20 
D)  $50 
E)  $100

Question 7

If the number of persons who attend the club meeting this week is X, then the number of people who will attend next week is 90 + 0.40X. What is a long-run equilibrium attendance for this club?

Accepted Answer

A)  225 
B)  150 
C)  180 
D)  90 
E)  60 
A)  225 
B)  150 
C)  180 
D)  90 
E)  60

Question 8

Big Pig and Little Pig have two possible strategies, Press the Button, and Wait at the Trough. If both pigs choose Wait at the Trough, both get 3. If both pigs choose Press the Button, then Big Pig gets 8 and Little Pig gets 2. If Little Pig presses the button and Big Pig waits at the trough, then Big Pig gets 10 and Little Pig gets 0. Finally, if Big Pig presses the button and Little Pig waits at the trough, then Big Pig gets 2 and Little Pig gets 1. In Nash equilibrium,

Accepted Answer

A)  Little Pig will get a payoff of 1 and Big Pig will get a payoff of 2. 
B)  Little Pig will get a payoff of 2 and Big Pig will get a payoff of 8. 
C)  both pigs will wait at the trough. 
D)  Little pig will get a payoff of zero. 
E)  the pigs must be using mixed strategies. 
A)  Little Pig will get a payoff of 1 and Big Pig will get a payoff of 2. 
B)  Little Pig will get a payoff of 2 and Big Pig will get a payoff of 8. 
C)  both pigs will wait at the trough. 
D)  Little pig will get a payoff of zero. 
E)  the pigs must be using mixed strategies.

Question 9

Two players are engaged in a game of Chicken. There are two possible strategies, Swerve and Drive Straight. A player who chooses to Swerve is called Chicken and gets a payoff of zero, regardless of what the other player does. A player who chooses to Drive Straight gets a payoff of 432 if the other player swerves and a payoff of -48 if the other player also chooses to Drive Straight. This game has two pure strategy equilibria and

Accepted Answer

A)  a mixed strategy equilibrium in which each player swerves with probability .10 and drives straight with probability .90. 
B)  a mixed strategy in which each player swerves with probability .05 and drives straight with probability .95. 
C)  a mixed strategy equilibrium in which one player swerves with probability .10 and the other swerves with probability .90. 
D)  two mixed strategies in which players alternate between swerving and driving straight. 
E)  no mixed strategies. 
A)  a mixed strategy equilibrium in which each player swerves with probability .10 and drives straight with probability .90. 
B)  a mixed strategy in which each player swerves with probability .05 and drives straight with probability .95. 
C)  a mixed strategy equilibrium in which one player swerves with probability .10 and the other swerves with probability .90. 
D)  two mixed strategies in which players alternate between swerving and driving straight. 
E)  no mixed strategies.

Question 10

If a game does not have an equilibrium in pure strategies, then it will not have an equilibrium in mixed strategies either.

Accepted Answer

A) True 
 B)False

Question 11

Professor Binmore has a monopoly in the market for undergraduate game theory textbooks. The time-discounted value of Professor Binmore's future earnings is $2,000. Professor Ditt is considering writing a book to compete with Professor Binmore's book. With two books amicably splitting the market, the time-discounted value of each professor's future earnings would be $200. If there is full information (each professor knows the profits of the other), under what conditions could Professor Binmore deter the entry of Professor Ditt into his market?

Accepted Answer

A)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $200. In so doing, Professor Binmore would loose $20 over time. 
B)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $20. In so doing, Professor Binmore would just break even over time. 
C)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would loose $2. In so doing, Professor Binmore would still make $190 over time. 
D)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would only make $2. In so doing, Professor Binmore would still make $100 over time. 
E)  None of the above. 
A)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $200. In so doing, Professor Binmore would loose $20 over time. 
B)  Professor Binmore threatens to cut his price so that Professor Ditt would loose $20. In so doing, Professor Binmore would just break even over time. 
C)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would loose $2. In so doing, Professor Binmore would still make $190 over time. 
D)  Professor Binmore threatens to cut his price and attack the credibility of Professor Ditt's book so that Professor Ditt would only make $2. In so doing, Professor Binmore would still make $100 over time. 
E)  None of the above.

Question 12

A dominant strategy equilibrium is a set of choices such that each player's choices are optimal regardless of what the other players choose.

Accepted Answer

A) True 
 B)False

Question 13

Suppose that in a Hawk-Dove game similar to the one discussed in your workbook, the payoff to each player is -6 if both play Hawk. If both play Dove, the payoff to each player is 3, and if one plays Hawk and the other plays Dove, the one that plays Hawk gets a payoff of 8 and the one that plays Dove gets 0. In equilibrium, we would expect hawks and doves to do equally well. This happens when the proportion of the total population that plays Hawk is

Accepted Answer

A)  .45. 
B)  .23. 
C)  .11. 
D)  .73. 
E)  1. 
A)  .45. 
B)  .23. 
C)  .11. 
D)  .73. 
E)  1.

Question 14

A famous Big Ten football coach had only two strategies, Run the ball to the left side of the line and Run the ball to the right side. The defense can concentrate forces on the left side or the right side. If the opponent concentrates on the wrong side, his offense is sure to gain at least 5 yards. If the defense defended the left side and the offense ran left, the offense gained only 1 yard. If the opponent defended the right side when the offense ran right, the offense would still gain at least 5 yards with probability .30. It is the last play of the game and the famous coach's team is on offense. If it makes 5 yards or more, it wins; if not, it loses. Both sides choose Nash equilibrium strategies. In equilibrium the offense

Accepted Answer

A)  is sure to run to the right side. 
B)  will run to the right side with probability .59. 
C)  will run to the right side with probability .74. 
D)  will run to the two sides with equal probability. 
E)  will run to the right side with probability .70. 
A)  is sure to run to the right side. 
B)  will run to the right side with probability .59. 
C)  will run to the right side with probability .74. 
D)  will run to the two sides with equal probability. 
E)  will run to the right side with probability .70.

Exam 27: Game Theory

In the prisoner's dilemma game, if each prisoner believed that the other prisoner would deny the crime, then both would deny the crime.

In a Nash equilibrium, everyone must be playing a dominant strategy.

If the number of persons who attend the club meeting this week is X, then the number of people who will attend next week is 90 + 0.40X. What is a long-run equilibrium attendance for this club?

If a game does not have an equilibrium in pure strategies, then it will not have an equilibrium in mixed strategies either.

A dominant strategy equilibrium is a set of choices such that each player's choices are optimal regardless of what the other players choose.

Budget Constraint

A: Budget Constraint

Preferences

A: Preferences

Utility

A: Utility

Choice

A: Choice

Demand

A: Demand

Revealed Preference

A: Revealed Preference

Slutsky Equation

A: Slutsky Equation

Buying and Selling

A: Buying and Selling

Intertemporal Choice

A: Intertemporal Choice

Asset Markets

A: Asset Markets

Uncertainty

A: Uncertainty

Risky Assets

A: Risky Assets

Consumers Surplus

A: Consumers Surplus

Market Demand

A: Market Demand

Equilibrium

A: Equilibrium

Auctions

A: Auctions

Technology

A: Technology

Profit Maximization

A: Profit Maximization

Cost Minimization

A: Cost Minimization

Cost Curves

A: Cost Curves

Firm Supply

A: Firm Supply

Industry Supply

A: Industry Supply

Monopoly

A: Monopoly

Monopoly Behavior

A: Monopoly Behavior

Factor Markets

A: Factor Markets

Oligopoly

A: Oligopoly

A: Game Theory

Game Applications

A: Game Applications

Behavioral Economics

Exchange

A: Exchange

Production

A: Production

Welfare

A: Welfare

Externalities

A: Externalities

Information Technology

A: Information Technology

Public Goods

A: Public Goods

Asymmetric Information

A: Asymmetric Information

Filters