Exam 7: Continuous Probability Distributions
Exam 1: Overview of Statistics52 Questions
Exam 2: Data Collection111 Questions
Exam 3: Describing Data Visually108 Questions
Exam 4: Descriptive Statistics150 Questions
Exam 5: Probability123 Questions
Exam 6: Discrete Probability Distributions126 Questions
Exam 7: Continuous Probability Distributions120 Questions
Exam 8: Sampling Distributions and Estimation106 Questions
Exam 9: One-Sample Hypothesis Tests147 Questions
Exam 10: Two-Sample Hypothesis Tests113 Questions
Exam 11: Analysis of Variance126 Questions
Exam 12: Simple Regression135 Questions
Exam 13: Multiple Regression130 Questions
Exam 14: Time Series Analysis114 Questions
Exam 15: Chi-Square Tests99 Questions
Exam 16: Nonparametric Tests85 Questions
Exam 17: Quality Management108 Questions
Select questions type
A company employs 300 employees. Each year, there is a 30 percent turnover rate for employees. We want to do a normal approximation to the binomial distribution of the number of employees who leave each year. For this normal approximation, the mean is ______ and the standard deviation is _____.
(Multiple Choice)
4.7/5  (37)
(37)
The triangular distribution T(10, 20, 50) has a standard deviation of:
(Multiple Choice)
4.8/5  (27)
(27)
The exponential distribution describes the number of arrivals per unit of time.
(True/False)
4.8/5  (45)
(45)
Assume that X is normally distributed with a mean μ = $64. Given that P(X ≥ $75) = 0.2981, we can calculate that the standard deviation of X is approximately:
(Multiple Choice)
4.8/5  (38)
(38)
The MPG (miles per gallon) for a certain compact car is normally distributed with a mean of 31 and a standard deviation of 0.8. What is the probability that the MPG for a randomly selected compact car would be less than 32?
(Multiple Choice)
4.8/5  (32)
(32)
If arrivals occur at a mean rate of 1.6 events per minute, the exponential probability of waiting less than 1 minute for the next arrival is:
(Multiple Choice)
5.0/5  (31)
(31)
A continuous uniform distribution U(0, 800) will have μ = 400 and σ = 230.94.
(True/False)
4.8/5  (42)
(42)
The true proportion of accounts receivable with some kind of error is 4 percent for Venal Enterprises. If an auditor randomly samples 50 accounts receivable, it is acceptable to use the normal approximation to estimate the probability that fewer than two will contain errors.
(True/False)
4.8/5  (34)
(34)
The mean, median, and mode of a normal distribution will always be the same.
(True/False)
4.9/5  (38)
(38)
If the mean waiting time for the next arrival is 12 minutes, what is the median waiting time?
(Multiple Choice)
4.8/5  (28)
(28)
Regarding continuous probability distributions, which statement is incorrect?
(Multiple Choice)
4.9/5  (33)
(33)
On average, 15 minutes elapse between discoveries of fraudulent corporate tax returns in a certain IRS office. What is the probability that less than 30 minutes will elapse before the next fraudulent corporate tax return is discovered?
(Multiple Choice)
4.9/5  (35)
(35)
Exam scores were normal in MIS 200. Jason's exam score was 1.41 standard deviations above the mean. What percentile is he in?
(Multiple Choice)
4.9/5  (43)
(43)
Which probability model is most appropriate to describe the waiting time (working days) until an office photocopier breaks down (i.e., requires unscheduled maintenance)?
(Multiple Choice)
4.9/5  (41)
(41)
The figure shows a standard normal N(0, 1) distribution. Find the z value for the shaded area. 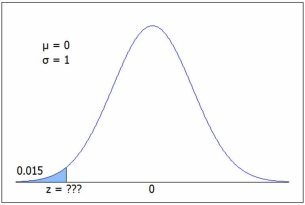 C.2 gives P(z < -2.17) = .0150 or use Excel =NORM.S.INV(0.015) = -2.17.
C.2 gives P(z < -2.17) = .0150 or use Excel =NORM.S.INV(0.015) = -2.17.
(Multiple Choice)
4.8/5  (38)
(38)
The exponential distribution is continuous and the Poisson distribution is discrete, yet the two distributions are closely related.
(True/False)
4.9/5  (42)
(42)
The figure shows a normal N(400, 23) distribution. Find the x value for the shaded area. 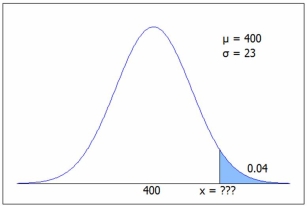 C.2 we get P(z > 1.75) = .0401, so x = µ + zσ = 400 + 1.75(23) = 440.3, or from Excel =NORM.INV(0.96,400,23) = 440.3.
C.2 we get P(z > 1.75) = .0401, so x = µ + zσ = 400 + 1.75(23) = 440.3, or from Excel =NORM.INV(0.96,400,23) = 440.3.
(Multiple Choice)
4.9/5  (41)
(41)
In Melanie's Styling Salon, the time to complete a simple haircut is normally distributed with a mean of 25 minutes and a standard deviation of 4 minutes. What percentage of customers require less than 32 minutes for a simple haircut?
(Multiple Choice)
4.8/5  (34)
(34)
The probability is .80 that a standard normal random variable is between -z and +z. The value of z is approximately:
(Multiple Choice)
4.8/5  (22)
(22)
The figure shows a normal N(400, 23) distribution. Find the x value for the shaded area. 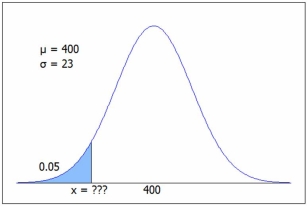 C.2 we get P(z < -1.645) = .05, so x = µ + zσ = 400 - 1.645(23) = 362.2, or from Excel =NORM.INV(0.05,400,23) = 362.2.
C.2 we get P(z < -1.645) = .05, so x = µ + zσ = 400 - 1.645(23) = 362.2, or from Excel =NORM.INV(0.05,400,23) = 362.2.
(Multiple Choice)
4.9/5  (32)
(32)
Showing 21 - 40 of 120
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)