Chat with AIExam 7: Linear Programming Under Uncertainty
Ken and Larry,Inc.,supplies its ice cream parlors with three flavors of ice cream: chocolate,vanilla,and banana.Due to extremely hot weather and a high demand for its products,the company has run short of its supply of ingredients: milk,sugar,and cream.Hence,they will not be able to fill all the orders received from their retail outlets,the ice cream parlors.Due to these circumstances,the company has decided to choose the amount of each flavor to produce that will maximize total profit,given the constraints on supply of the basic ingredients.The chocolate,vanilla,and banana flavors generate,respectively,$1.00,$0.90,and $0.95 of profit per gallon sold.The company has only 200 gallons of milk,150 pounds of sugar,and 60 gallons of cream left in its inventory.The linear programming formulation for this problem is shown below in algebraic form.Let C = gallons of chocolate ice cream produced,V = gallons of vanilla ice cream produced,B = gallons of banana ice cream produced.Maximize Profit = 1.00 C + 0.90 V + 0.95 B,subject to Milk: 0.45 C + 0.50 V + 0.40 B ≤ 200 gallons Sugar: 0.50 C + 0.40 V + 0.40 B ≤ 150 pounds Cream: 0.10 C + 0.15 V + 0.20 B ≤ 60 gallons and C ≥ 0,V ≥ 0,B ≥ 0.This problem was solved using the Excel Solver.The spreadsheet (already solve d)Suppose the company discovers that 3 gallons of cream have gone sour and so must be thrown out.Will the optimal solution change,and what can be said about the effect on total profit? (e)Suppose the company has the opportunity to buy an additional 15 pounds of sugar at a total cost of $15.Should they? Explain.(f)Fill in all the sensitivity report information for the milk constraint,given just the optimal solution for the problem.Explain how you were able to deduce each number.d)and the sensitivity report are shown below.[Note: The numbers in the sensitivity report for the milk constraint are missing on purpose,since you will be asked to fill in these numbers in part (f).] ![Ken and Larry,Inc.,supplies its ice cream parlors with three flavors of ice cream: chocolate,vanilla,and banana.Due to extremely hot weather and a high demand for its products,the company has run short of its supply of ingredients: milk,sugar,and cream.Hence,they will not be able to fill all the orders received from their retail outlets,the ice cream parlors.Due to these circumstances,the company has decided to choose the amount of each flavor to produce that will maximize total profit,given the constraints on supply of the basic ingredients.The chocolate,vanilla,and banana flavors generate,respectively,$1.00,$0.90,and $0.95 of profit per gallon sold.The company has only 200 gallons of milk,150 pounds of sugar,and 60 gallons of cream left in its inventory.The linear programming formulation for this problem is shown below in algebraic form.Let C = gallons of chocolate ice cream produced,V = gallons of vanilla ice cream produced,B = gallons of banana ice cream produced.Maximize Profit = 1.00 C + 0.90 V + 0.95 B,subject to Milk: 0.45 C + 0.50 V + 0.40 B ≤ 200 gallons Sugar: 0.50 C + 0.40 V + 0.40 B ≤ 150 pounds Cream: 0.10 C + 0.15 V + 0.20 B ≤ 60 gallons and C ≥ 0,V ≥ 0,B ≥ 0.This problem was solved using the Excel Solver.The spreadsheet (already solve d)Suppose the company discovers that 3 gallons of cream have gone sour and so must be thrown out.Will the optimal solution change,and what can be said about the effect on total profit? (e)Suppose the company has the opportunity to buy an additional 15 pounds of sugar at a total cost of $15.Should they? Explain.(f)Fill in all the sensitivity report information for the milk constraint,given just the optimal solution for the problem.Explain how you were able to deduce each number.d)and the sensitivity report are shown below.[Note: The numbers in the sensitivity report for the milk constraint are missing on purpose,since you will be asked to fill in these numbers in part (f).] For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?](https://storage.examlex.com/TB2462/11ea84c6_c86c_8e71_83dc_8f89fb721873_TB2462_00.jpg)
For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?
For each of the following parts,answer the question as specifically and completely as is possible without solving the problem again on the Excel Solver.Note: Each part is independent (i.e.,any change made to the model in one part does not apply to any other parts).(a)What is the optimal solution and total profit? (b)Suppose the profit per gallon of banana changes to $1.00.Will the optimal solution change,and what can be said about the effect on total profit? (c)Suppose the profit per gallon of banana changes to 92¢.Will the optimal solution change,and what can be said about the effect on total profit?
(40) 
Verified(a)The optimal solution is to produce no chocolate ice cream,300 gallons of vanilla ice cream,and 75 gallons of banana ice cream.Total profit will be $341.25.(b)The optimal solution will change since $1.00 is outside the allowable range of $(0.95-0.05)to $(0.95 + 0.021429).The profit will go up,but how much can't be determined without re-solving.(c)The optimal solution will not change since $0.92 is within the allowable range.The total profit will decrease by (75)$0.03 = $2.25 to $339.(d)The optimal solution will change.Since the change is within the allowable range (the allowable decrease is 3.75),we can calculate the change in profit using the shadow price (1*3 = 3).The new profit will be $338.25.(e)This increase is outside of the allowable increase of 10,so the problem will have be re-solved to determine whether this is worthwhile.(f)The final value is 180 as shown in the totals column in the solution.The shadow price is 0 since we are using less milk than we have available.The right-hand side value is 200 as given in the problem.The allowable increase is infinity since we are already using less than is available.The allowable decrease is 20 since the solution will change once the right-hand side drops below 180.
A certain linear programming problem has four functional constraints in inequality form such that their right-hand sides (the bi)are uncertain parameters.Therefore,chance constraints with = 0.95 have been introduced in place of these constraints.After next substituting the deterministic equivalents of these chance constraints and solving the resulting new linear programming model,its optimal solution is found to satisfy two of these deterministic equivalents with equality whereas there is some slack in the other two deterministic equivalents.Determine the lower bound and the upper bound on the probability that all of these four original constraints will turn out to be satisfied by the optimal solution for the new linear programming model so this solution actually will be feasible for the original problem.
(33) VerifiedFor each of the two functional constraints whose deterministic equivalent is satisfied with equality by the optimal solution for the new linear programming model,the probability is exactly = 0.95 that this constraint will be satisfied by this optimal solution.For each of the other two constraints,this probability can be anywhere between 0.95 and 1.Therefore,by using 1 for this probability,the desired upper bound is Upper bound = (0.95)2 = 0.9025.However,by using 0.95 for this probability,the desired lower bound is Lower bound = (0.95)4 = 0.8145.
Stickley Furniture is a manufacturer of fine hand-crafted furniture.During the next production period,management is considering producing dining room tables,dining room chairs,and/or bookcases.The time required for each item to go through the two stages of production (assembly and finishing),the amount of wood required (fine cherry wood)Suppose a worker in the assembly department calls in sick,so eight fewer hours now are available in the assembly department.How much would this affect total profit? Would it change the optimal production quantities? (e)Explain why the shadow price for the wood constraint is zero.(f)A new worker has been hired who is trained to do both assembly and finishing.She will split her time between the two areas,so there now are four additional hours available in both assembly and finishing.How much would this affect total profit? Would this change the optimal production quantities? (g)Based on the sensitivity report,is it wise to have the new worker in part f split her time equally between assembly and finishing,or would some other plan be better? (h)Use a parameter analysis report to determine how the optimal production quantities and total profit will change depending on how the new worker in part f allocates her time between assembly and finishing.In particular,assume 0,1,2,...,or 8 hours are added to assembly,with a corresponding 8,7,6,...,or 0 hours added to finishing.d),and the corresponding unit profits are given in the following table,along with the amount of each resource available in the upcoming production period.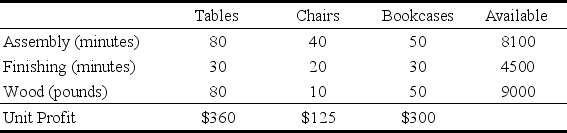 
After formulating a linear programming model to determine the production levels that would maximize profit,the solved model and the corresponding sensitivity report are shown below.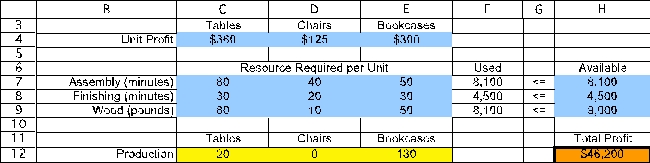 
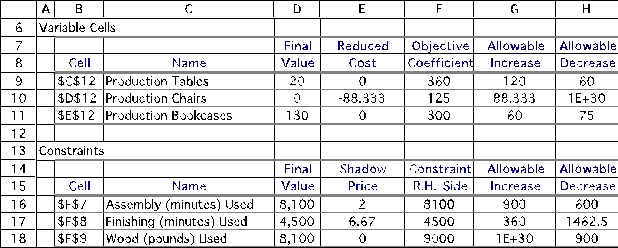(a)Suppose the profit per table increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (b)Suppose the profit per chair increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (c)Suppose the profit per table increases by $90 and the profit per bookcase decreases by $50.Will this change the optimal production quantities? What can be said about the change in total profit?
After formulating a linear programming model to determine the production levels that would maximize profit,the solved model and the corresponding sensitivity report are shown below. (a)Suppose the profit per table increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (b)Suppose the profit per chair increases by $100.Will this change the optimal production quantities? What can be said about the change in total profit? (c)Suppose the profit per table increases by $90 and the profit per bookcase decreases by $50.Will this change the optimal production quantities? What can be said about the change in total profit? (36) Verified(a)No.The increase of $100 is less than the allowable increase for the profit per table of $120.Therefore,the optimal production quantities will stay the same.The total profit will increase by $100 per table produced,or (20)($100)= $2000,to a total profit of $48,200.(b)Yes.The increase of $100 is more than the allowable increase for the profit per chair of $88.33.Therefore,the optimal production quantities will change.The total profit will likely increase,but the amount it will increase cannot be determined without re-solving.(c)$90 is 90/120 = 75% of the allowable increase for tables.$50 is 50/75 = 66.7% of the allowable decrease for bookcases.75% + 66.7% > 100%.Therefore,the optimal solution may or may not change.We can't determine the new profit without re-solving.(d)The decrease of 8 hours = 480 minutes is within the allowable decrease for assembly of 600 minutes.Therefore the shadow price of $2 is valid.The change in profit is equal to the shadow price times the change in the right-hand-side or ($2)(-480 minutes)= -$960.Therefore,the total profit decreases by $960 to $45,240.The current optimal solution used all of the available assembly time,so the production quantities must change with the decrease in available assembly time.(e)The current optimal solution uses only 8,100 out of the available 9,000 pounds of wood.Therefore,there are 900 pounds of slack in this constraint.Adding more wood or taking a small amount of wood away will not change the optimal solution or the total profit because the current optimal solution isn't using all of the wood anyway.(f)4 hours = 240 minutes is 240/900 = 26.7% of the allowable increase for assembly time.4 hours = 240 minutes is 240/360 = 66.7% of the allowable increase for finishing.26.7% + 66.7% < 100%,so the 100% rule says that both shadow prices are valid.The increase in profit is therefore Change in Profit = (Shadow Price)(Change in Right-Hand-Side)= ($2)(240)+ ($6.67)(240)= $480 + $1,600 = $2,080.Therefore,profit will increase by $2,080 to $48,280.The optimal production quantities will change to take advantage of the extra hours and this increased profit.(g)The shadow price is higher for finishing than assembly.Thus,the profit will increase if more hours are devoted to finishing rather than assembly.However,after 360 minutes (6 hours)are added to assembly,the allowable increase is exceeded and the shadow price will change.Depending on what the shadow price changes to,it would either be advisable to devote all 8 hours to assembly (if the new shadow price is still greater than $2),or devote 6 hours to assembly and 2 hours to finishing (if the new shadow price is less than $2).(h)The original spreadsheet needs to be modified to account for the extra minutes available in assembly and finishing.The total extra minutes for assembly are put into a data cell in J3.Cell J7 is defined as an optimization parameter by choosing Optimization from the Parameters menu on the Analytic Solver Platform tab,and specifying a lower limit of 0 and an upper limit of 480.The extra minutes left over for finishing are then calculated in J8.These extra minutes are accounted for in the total available minutes in H7:H8.Next,a parameter analysis report is run by choosing Optimization>Parameter Analysis from the Reports menu of the Analytic Solver Platform tab.All results cells and all parameter cells are chosen,and 9 major axis points are specified.The parameter analysis report generated below is then created by ASPE.(Note,an extra column was created to also show the extra finishing time,and the labels in the first row were modified.)From the parameter analysis report,the highest profit is achieved when 1 hour is allocated to assembly and 7 hours to finishing.A little trial and error reveals that the highest profit is achieved with 75 minutes allocated to assembly and 405 minutes allocated to finishing.
Consider the following problem.Maximize Z = 20x1 + c2x2,subject to 3x1 + a12x2 ≥ 60 5x2 + a22x2 ≤ 100 and x1 ≥ 0,x2 ≥ 0,where x1 represents the level of activity 1 and x2 represents the level of activity 2.The values of c2,a12,and a22 have not been determined yet.Only activity 1 needs to be undertaken soon whereas activity 2 will be initiated somewhat later.There are two different,but equally likely,scenarios that could unfold between now and the time activity 2 is undertaken that would lead to different values for c2,a12,and a22,as listed below.Scenario 1: c2 = 30,a12 = 4,and a22 = 7 Scenario 2: c2 = 10,a12 = 1,and a22 = 3 The goal is to use all of this information to choose a value for x1 now and to simultaneously determine a plan for choosing a value of x2 later after seeing which scenario has occurred.Use stochastic programming with recourse to formulate the appropriate model for this problem.
(38) Consider the following problem.Maximize Z = 3x1 + x2 + 2x3,subject to x1 - x2 + 2x3 ≤ 20 2x1 + x2 - x3 ≤ 10 and x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.Let x4 and x5 denote the slack variables for the respective functional constraints.After we apply the simplex method,the final simplex tableau is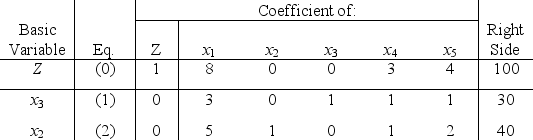 
(a)Perform sensitivity analysis to determine which of the 11 parameters of the model are sensitive parameters in the sense that even small changes in just that parameter's value might change the optimal solution.
(b)Use algebraic analysis to find the allowable range to stay optimal for each cj..
(c)Use algebraic analysis to find the allowable range for each bi.
(a)Perform sensitivity analysis to determine which of the 11 parameters of the model are sensitive parameters in the sense that even small changes in just that parameter's value might change the optimal solution.
(b)Use algebraic analysis to find the allowable range to stay optimal for each cj..
(c)Use algebraic analysis to find the allowable range for each bi. (34) Consider the following model.Minimize Z = c1x1 + c2x2,subject to a11x1 + a12x2 ≥ b1 a21x2 + a22x2 ≤ b2 and x1 ≥ 0,x2 ≥ 0.The estimates and ranges of uncertainty for the parameters are shown in the following table.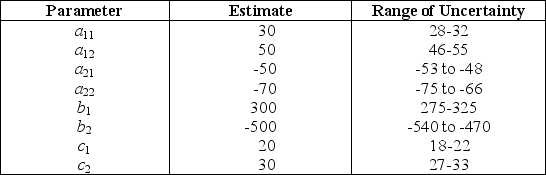 
Use robust optimization to formulate a conservative version of this model.
Use robust optimization to formulate a conservative version of this model. (37) Consider the following problem.Maximize Z = 3x1 + 4x2 + 8x3,subject to 2x1 + 3x2 + 5x3 ≤ 9 x1 + 2x2 + 3x3 ≤ 5 and x1 ≥ 0,x2 ≥ 0,x3 ≥ 0.Let x4 and x5 denote the slack variables for the respective functional constraints.After we apply the simplex method,the final simplex tableau is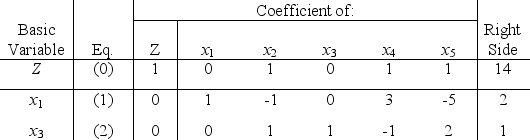 
While doing postoptimality analysis,you learn that some of the parameter values used in the original model just given are just rough estimates,where the range of likely values in each case is within ± 50 percent of the values used here.For each of the following parameters,perform sensitivity analysis to determine whether this uncertainty might affect either the feasibility or the optimality of the above basic solution.Specifically,for each parameter,determine the allowable range of values for which the current basic solution (perhaps with new values for the basic variables)will remain both feasible and optimal.Then,for each parameter and its range of likely values,indicate which part of this range lies within the allowable range and which parts correspond to values for which the current basic solution will no longer be both feasible and optimal.(a)Parameter b2 (b)Parameter c2 (c)Parameter a22 d)Parameter c3 (e)Parameter a12 (f)Parameter b1
While doing postoptimality analysis,you learn that some of the parameter values used in the original model just given are just rough estimates,where the range of likely values in each case is within ± 50 percent of the values used here.For each of the following parameters,perform sensitivity analysis to determine whether this uncertainty might affect either the feasibility or the optimality of the above basic solution.Specifically,for each parameter,determine the allowable range of values for which the current basic solution (perhaps with new values for the basic variables)will remain both feasible and optimal.Then,for each parameter and its range of likely values,indicate which part of this range lies within the allowable range and which parts correspond to values for which the current basic solution will no longer be both feasible and optimal.(a)Parameter b2 (b)Parameter c2 (c)Parameter a22 d)Parameter c3 (e)Parameter a12 (f)Parameter b1 (31) 
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)