Exam 11: Dynamic Programming
Consider the following nonlinear programming problem.Maximize Z = 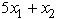 ,subject to 2
,subject to 2 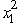 +
+ 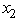 ≤ 13
≤ 13 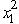 +
+ 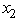 ≤ 9 and
≤ 9 and 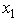 ≥ 0,
≥ 0, 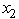 ≥ 0.Use dynamic programming to solve this problem.
≥ 0.Use dynamic programming to solve this problem.
The two stages involve making the decisions on the values of the two variables in order.At stage n,let the state sn be the vector (R1,R2),where Ri is the slack in the i-th constraint,so s1 = (13,9)and s2 = (13 - 2 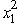 ,9 -
,9 - 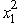 ).For stage 2 (the second variable),we have f2 (R1,R2, x2)= x2,0 x2 min{R1,R2},so
).For stage 2 (the second variable),we have f2 (R1,R2, x2)= x2,0 x2 min{R1,R2},so 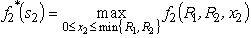 is easily solved,as shown in the following table.
is easily solved,as shown in the following table. 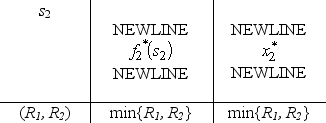 For stage 1 (the first variable),we now have f1(13,9, x1)=
For stage 1 (the first variable),we now have f1(13,9, x1)= 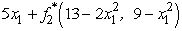 =
= 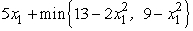 .For 0 x1 2,
.For 0 x1 2, 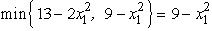 f1(13,9, x1)=
f1(13,9, x1)= 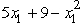 .Since
.Since 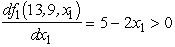 for 0 ≤ x1 ≤ 2,we now have
for 0 ≤ x1 ≤ 2,we now have 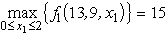 at x1 = 2.For x1 2,
at x1 = 2.For x1 2, 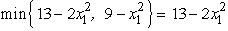 f1(13,9, x1)=
f1(13,9, x1)= 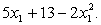 Since
Since 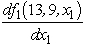 = 5 - 4x1 < 0 for x1 ≥ 0,it follows that
= 5 - 4x1 < 0 for x1 ≥ 0,it follows that 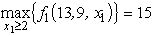 at x1 = 2.Since f1(13,9,x1)is maximized at x1 = 2 over both the range 0 ≤ x1 ≤ 2 and the range x1 ≥ 2,the maximum must be at x1 = 2 over the entire range of x1 ≥ 0.Consequently,
at x1 = 2.Since f1(13,9,x1)is maximized at x1 = 2 over both the range 0 ≤ x1 ≤ 2 and the range x1 ≥ 2,the maximum must be at x1 = 2 over the entire range of x1 ≥ 0.Consequently, 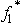 (13,9)=
(13,9)= 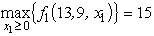 at
at 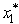 = 2.Therefore,since x1 = 2 leaves a slack of R1 = 13 - 2
= 2.Therefore,since x1 = 2 leaves a slack of R1 = 13 - 2 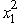 = 5 and R2 = 9 -
= 5 and R2 = 9 - 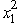 = 5 in the two constraints,so
= 5 in the two constraints,so 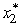 = min{R1,R2} = 5,the optimal solution for the overall problem is
= min{R1,R2} = 5,the optimal solution for the overall problem is 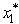 = 2,
= 2, 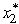 = 5,with Z* = 15.
= 5,with Z* = 15.
A company is planning its advertising strategy for next year for its three major products.Since the three products are quite different,each advertising effort will focus on a single product.In units of millions of dollars,a total of 6 is available for advertising next year,where the advertising expenditure for each product must be an integer greater than or equal to 1.The vice-president for marketing has established the objective: Determine how much to spend on each product in order to maximize total sales.The following table gives the estimated increase in sales (in appropriate units)for the different advertising expenditures. 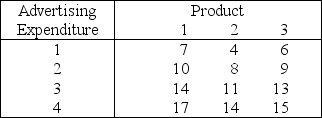 Use dynamic programming to solve this problem.
Use dynamic programming to solve this problem.
Since the decisions to be made are the advertising expenditures on the three products,the stages for a dynamic programming formulation of this problem correspond to the three products.When making the decision for a particular product,the essential information is the amount of the advertising budget still remaining,so this becomes the current state in this formulation.Let xn be the advertising dollars (in millions)spent on product n.Let sn be the amount of advertising budget remaining.Let 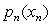 be the increase in sales of product n when xn million dollars are spent on product n,as given by the above table.Then,using the usual dynamic programming notation presented in Sec.10.2 of the textbook,the recursive relationship for this problem is
be the increase in sales of product n when xn million dollars are spent on product n,as given by the above table.Then,using the usual dynamic programming notation presented in Sec.10.2 of the textbook,the recursive relationship for this problem is 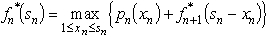 .The solution procedure now starts at the end (stage 3)and moves backward stage by stage.For n = 3,
.The solution procedure now starts at the end (stage 3)and moves backward stage by stage.For n = 3, 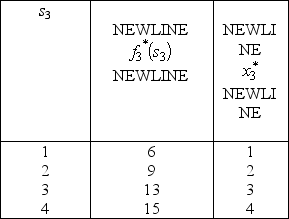 For n = 2,
For n = 2, 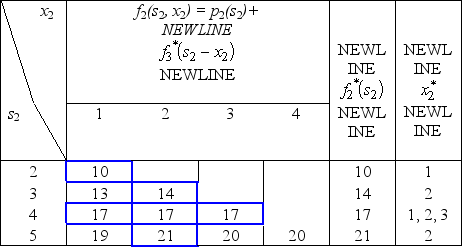 For n = 1,
For n = 1,  Hence,since s2 = 6 -
Hence,since s2 = 6 - 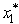 and s3 = s2 -
and s3 = s2 - 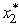 ,there are two optimal plans as given in the table below.
,there are two optimal plans as given in the table below. 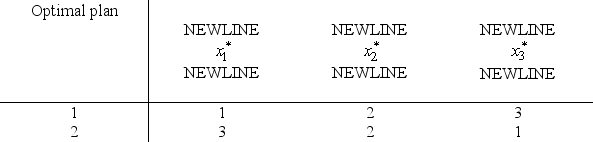
Consider the following nonlinear programming problem.Maximize Z = 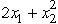 ,subject to
,subject to 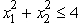 and
and 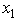 ≥ 0,
≥ 0, 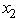 ≥ 0.Use dynamic programming to solve this problem.
≥ 0.Use dynamic programming to solve this problem.
The two stages involve making the decisions on the values of the two variables in order.At stage n,let the state sn be the remaining slack in the constraint 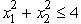 ,so s1 = 4 and s2 = 4 -
,so s1 = 4 and s2 = 4 - 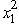 .For n = 2,
.For n = 2, 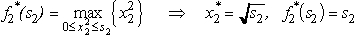 .For n = 1,
.For n = 1, 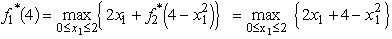 .To maximize (2x1 + 4 -
.To maximize (2x1 + 4 - 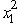 )over 0 ≤ x1 ≤ 2,we take the first and second derivatives.
)over 0 ≤ x1 ≤ 2,we take the first and second derivatives. 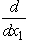 (2x1 + 4 -
(2x1 + 4 - 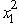 )= 2 - 2x1 = 0,so x1 = 1 is a critical point.
)= 2 - 2x1 = 0,so x1 = 1 is a critical point. 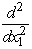 (2x1 + 4 -
(2x1 + 4 - 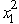 )= -2,so x1 = 1 is indeed the maximum over 0 ≤ x1 ≤ 2.Since x1 = 1 leaves a slack of
)= -2,so x1 = 1 is indeed the maximum over 0 ≤ x1 ≤ 2.Since x1 = 1 leaves a slack of 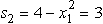 in the constraint,the overall optimal solution is
in the constraint,the overall optimal solution is 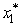 = 1,
= 1, 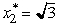 ,with Z* = 5.
,with Z* = 5.
The management of a company is considering three possible new products for next year's product line.A decision now needs to be made regarding which products to market and at what production levels.Initiating the production of two of these products would require a substantial start-up cost,as shown in the first row of the table below.Once production is under way,the marginal net revenue from each unit produced is shown in the second row.The third row gives the percentage of the available production capacity that would be used for each unit produced. 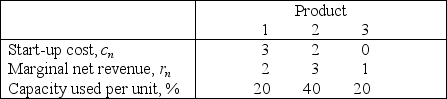 Only 3 units of product 1 could be sold,whereas all units that could be produced of the other two products could be sold.The objective is to determine the number of units of each product to produce in order to maximize the total profit (total net revenue minus start-up costs).(a)Assuming that production quantities must be integers,use dynamic programming to solve this problem.(b)Now consider the case where the divisibility assumption holds so that the variables representing production quantities are treated as continuous variables.Assuming that proportionality holds for both net revenues and capacities used,use dynamic programming to solve this problem.
Only 3 units of product 1 could be sold,whereas all units that could be produced of the other two products could be sold.The objective is to determine the number of units of each product to produce in order to maximize the total profit (total net revenue minus start-up costs).(a)Assuming that production quantities must be integers,use dynamic programming to solve this problem.(b)Now consider the case where the divisibility assumption holds so that the variables representing production quantities are treated as continuous variables.Assuming that proportionality holds for both net revenues and capacities used,use dynamic programming to solve this problem.
Consider the following integer nonlinear programming problem.Maximize Z = 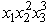 ,subject to
,subject to 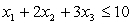
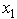 ≥ 1,
≥ 1, 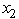 ≥ 1,
≥ 1, 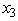 ≥ 1,and
≥ 1,and 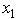 ,
, 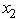 ,
, 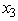 are integers.Use dynamic programming to solve this problem.
are integers.Use dynamic programming to solve this problem.
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)