Exam 19: Markov Decision Processes

A soap company specializes in a luxury type of bath soap.The sales of this soap fluctuate between two levels - low and high - depending upon two factors: (1)whether they advertise and (2)the advertising and marketing of new products by competitors.The second factor is out of the company's control,but it is trying to determine what its own advertising policy should be.For example,the marketing manager's proposal is to advertise when sales are low but not to advertise when sales are high (a particular policy).Advertising in any quarter of a year has primary impact on sales in the following quarter.At the beginning of each quarter,the needed information is available to forecast accurately whether sales will be low or high that quarter and to decide whether to advertise that quarter.The cost of advertising is $1 million for each quarter of a year in which it is done.When advertising is done during a quarter,the probability of having high sales the next quarter is 1/2 or 3/4 depending upon whether the current quarter's sales are low or high.These probabilities go down to 1/4 or 1/2 when advertising is not done during the current quarter.The company's quarterly profits (excluding advertising costs)are $4 million when sales are high but only $2 million when sales are low.Management now wants to determine the advertising policy that will maximize the company's (long-run)expected average net profit (profit minus advertising costs)per quarter.(a)Formulate this problem as a Markov decision process by identifying the states and decisions and then finding the 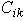(b)Identify all the (stationary deterministic)policies.For each one,find the transition matrix and write an expression for the (long-run)expected average net profit per quarter in terms of the unknown steady-state probabilities ( 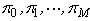(c)Formulate a linear programming model for finding an optimal policy.d)Use the policy improvement algorithm described in Supplement 1 to Chapter 19 to find an optimal policy when starting with an initial policy of never advertising.

4.9/5

(36)

Correct Answer:

Verified

Solution of Value Determination Equations: g(R1)= -2.67 v0(R1)= 2.667 v1(R1)= 0 Policy Improvement: State 0: -2 + 0.75(2.667)+ (0)- (2.667)= -2.67 for decision 1 -1 + 0.5 (2.667)+ (0)- (2.667)= -2.33 for decision 2 State 1: -4 + 0.50(2.667)+ (0)- (0)= -2.67 for decision 1 -3 + 0.25(2.667)+ (0)- (0)= -2.33 for decision 2 The minimum for both states is achieved by using decision 1 (don't advertise).Since this policy is identical to the preceding policy (the initial policy),it must be an optimal policy.Optimal Policy: d0(R2)= 1 d1(R2)= 1 g(R1)= -2.67 v0(R1)= 2.667 v1(R1)= 0