Question 1

Assuming that each of the 52 cards in an ordinary deck has a probability of 1/52 of being drawn, what is the probability of drawing a black ace?

Accepted Answer

A) 1/52 
B) 2/52 
C) 3/52 
D) 4/52 
A) 1/52 
B) 2/52 
C) 3/52 
D) 4/52

Question 2

If P(A) = 0.45, P(B) = 0.55, and P(A $\cup$ B) = 0.78, then P(A | B) =

Accepted Answer

A) zero 
B) 0.45 
C) 0.22 
D) 0.40 
A) zero 
B) 0.45 
C) 0.22 
D) 0.40

Question 3

As a company manager for Claimstat Corporation there is a 0.40 probability that you will be promoted this year. There is a 0.72 probability that you will get a promotion, a raise, or both. The probability of getting a promotion and a raise is 0.25.
a.If you get a promotion, what is the probability that you will also get a raise?
b.What is the probability that you will get a raise?
c.Are getting a raise and being promoted independent events? Explain using probabilities.
d.Are these two events mutually exclusive? Explain using probabilities.

Accepted Answer

a.0.625
b.0.57
c.No,

Question 4

If A and B are independent events with P(A) = 0.35 and P(B) = 0.20, then, P(A $\cup$ B) =

Accepted Answer

A) 0.07 
B) 0.62 
C) 0.55 
D) 0.48 
A) 0.07 
B) 0.62 
C) 0.55 
D) 0.48

Question 5

In a city, 60% of the residents live in houses and 40% of the residents live in apartments. Of the people who live in houses, 20% own their own business. Of the people who live in apartments, 10% own their own business. If a person owns his or her own business, find the probability that he or she lives in a house.

Accepted Answer

The answer of In a city, 60% of the residents...

Question 6

If two events are mutually exclusive, then their intersection

Accepted Answer

A) will be equal to zero 
B) can have any value larger than zero 
C) must be larger than zero, but less than one 
D) will be one 
A) will be equal to zero 
B) can have any value larger than zero 
C) must be larger than zero, but less than one 
D) will be one

Question 7

When the results of experimentation or historical data are used to assign probability values, the method used to assign probabilities is referred to as the

Accepted Answer

A) relative frequency method 
B) subjective method 
C) classical method 
D) posterior method 
A) relative frequency method 
B) subjective method 
C) classical method 
D) posterior method

Question 8

In a recent survey in a Statistics class, it was determined that only 60% of the students attend class on Fridays. From past data it was noted that 98% of those who went to class on Fridays pass the course, while only 20% of those who did not go to class on Fridays passed the course.
a.What percentage of students is expected to pass the course?
b.Given that a person passes the course, what is the probability that he/she attended classes on Fridays?

Accepted Answer

The answer of In a recent survey in a Statistics...

Question 9

If A and B are mutually exclusive events with P(A) = 0.3 and P(B) = 0.5, then P(A $\cup$B) =

Accepted Answer

A) 0.00 
B) 0.15 
C) 0.8 
D) 0.2 
A) 0.00 
B) 0.15 
C) 0.8 
D) 0.2

Question 10

In a recent survey about appliance ownership, 58.3% of the respondents indicated that they own Maytag appliances, while 23.9% indicated they own both Maytag and GE appliances and 70.7% said they own at least one of the two appliances.
Define the events as
M = Owning a Maytag appliance
G = Owning a GE appliance
a.What is the probability that a respondent owns a GE appliance?
b.Given that a respondent owns a Maytag appliance, what is the probability that the respondent also owns a GE appliance?
c.Are events "M" and "G" mutually exclusive? Why or why not? Explain, using probabilities.
d.Are the two events "M" and "G" independent? Explain, using probabilities.

Accepted Answer

a.0.363
b.0.4099
c.No, the int

Question 11

If A and B are independent events with P(A) = 0.38 and P(B) = 0.55, then P(A | B) =

Accepted Answer

A) 0.209 
B) 0.000 
C) 0.550 
D) 0.38 
A) 0.209 
B) 0.000 
C) 0.550 
D) 0.38

Question 12

An applicant has applied for positions at Company A and Company B. The probability of getting an offer from Company A is 0.4, and the probability of getting an offer from Company B is 0.3. Assuming that the two job offers are independent of each other, what is the probability that
a.the applicant gets an offer from both companies?
b.the applicant will get at least one offer?
c.the applicant will not be given an offer from either company?
d.Company A does not offer her a job, but Company B does?

Accepted Answer

a.0.12
b.0

Question 13

Tammy is a general contractor and has submitted two bids for two projects (A and B). The probability of getting project A is 0.65. The probability of getting project B is 0.77. The probability of getting at least one of the projects is 0.90.
a.What is the probability that she will get both projects?
b.Are the events of getting the two projects mutually exclusive? Explain, using probabilities.
c.Are the two events independent? Explain, using probabilities.

Accepted Answer

a.0.52
b.No, the int

Question 14

The probability of the occurrence of event A in an experiment is 1/3. If the experiment is performed 2 times and event A did not occur, then on the third trial event A

Accepted Answer

A) must occur 
B) may occur 
C) could not occur 
D) has a 2/3 probability of occurring 
A) must occur 
B) may occur 
C) could not occur 
D) has a 2/3 probability of occurring

Question 15

An experiment consists of tossing 4 coins successively. The number of sample points in this experiment is

Accepted Answer

A) 16 
B) 8 
C) 4 
D) 2 
A) 16 
B) 8 
C) 4 
D) 2

Question 16

Assume you have applied for two scholarships, a Merit scholarship (M) and an Athletic scholarship (A). The probability that you receive an Athletic scholarship is 0.18. The probability of receiving both scholarships is 0.11. The probability of getting at least one of the scholarships is 0.3.
a.What is the probability that you will receive a Merit scholarship?
b.Are events A and M mutually exclusive? Why or why not? Explain.
c.Are the two events A, and M, independent? Explain, using probabilities.
d.What is the probability of receiving the Athletic scholarship given that you have been awarded the Merit scholarship?
e.
What is the probability of receiving the Merit scholarship given that you have been awarded the Athletic scholarship?

Accepted Answer

a.0.23
b.No, because

Question 17

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

Accepted Answer

A) smaller than the probability of tails 
B) larger than the probability of tails 
C) 1/16 
D) 1/2 
A) smaller than the probability of tails 
B) larger than the probability of tails 
C) 1/16 
D) 1/2

Question 18

An automobile dealer has kept records on the customers who visited his showroom. Forty percent of the people who visited his dealership were female. Furthermore, his records show that 35% of the females who visited his dealership purchased an automobile, while 20% of the males who visited his dealership purchased an automobile. Let
A1 = the event that the customer is female
A2 = the event that the customer is male
a.What is the probability that a customer entering the showroom will buy an automobile?
b.A car salesperson has just informed us that he sold a car to a customer. What is the probability that the customer was female?

Accepted Answer

Question 19

A survey of a sample of business students resulted in the following information regarding the genders of the individuals and their selected major.
Selected Major
   
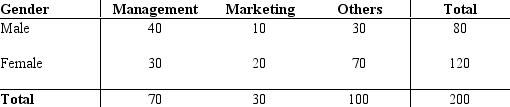a.What is the probability of selecting an individual who is majoring in Marketing?
b.What is the probability of selecting an individual who is majoring in Management, given that the person is female?
c.Given that a person is male, what is the probability that he is majoring in Management?
d.What is the probability of selecting a male individual?

Accepted Answer

a.0.15
b.0

Question 20

Records of a company show that 15% of the employees have only a high school diploma; 75% have bachelor degrees; and 10% have graduate degrees. Of those with only a high school diploma, 12% hold management positions; whereas, of those having bachelor degrees, 58% hold management positions. Finally, 82% of the employees who have graduate degrees hold management positions.
a.What percentage of employees holds management positions?
b.Given that a person holds a management position, what is the probability that she/he has a graduate degree?

Accepted Answer

The answer of Records of a company show that 15%...

Assuming that each of the 52 cards in an ordinary deck has a probability of 1/52 of being drawn, what is the probability of drawing a black ace?

If P(A) = 0.45, P(B) = 0.55, and P(A $\cup$ B) = 0.78, then P(A | B) =

If A and B are independent events with P(A) = 0.35 and P(B) = 0.20, then, P(A $\cup$ B) =

If two events are mutually exclusive, then their intersection

When the results of experimentation or historical data are used to assign probability values, the method used to assign probabilities is referred to as the

If A and B are mutually exclusive events with P(A) = 0.3 and P(B) = 0.5, then P(A $\cup$ B) =

If A and B are independent events with P(A) = 0.38 and P(B) = 0.55, then P(A | B) =

The probability of the occurrence of event A in an experiment is 1/3. If the experiment is performed 2 times and event A did not occur, then on the third trial event A

An experiment consists of tossing 4 coins successively. The number of sample points in this experiment is

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

Data and Statistics

Descriptive Statistics: Tabular and Graphical Presentations

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Comparisons Involving Means, Experimental Design and Analysis of Variance

Comparisons Involving Proportions and a Test of Independence

Simple Linear Regression

Multiple Regression

Filters

Exam 4: Introduction to Probability

Assuming that each of the 52 cards in an ordinary deck has a probability of 1/52 of being drawn, what is the probability of drawing a black ace?

If P(A) = 0.45, P(B) = 0.55, and P(A ∪\cup∪ B) = 0.78, then P(A | B) =

If A and B are independent events with P(A) = 0.35 and P(B) = 0.20, then, P(A ∪\cup∪ B) =

If two events are mutually exclusive, then their intersection

When the results of experimentation or historical data are used to assign probability values, the method used to assign probabilities is referred to as the

If A and B are mutually exclusive events with P(A) = 0.3 and P(B) = 0.5, then P(A ∪\cup∪ B) =

If A and B are independent events with P(A) = 0.38 and P(B) = 0.55, then P(A | B) =

The probability of the occurrence of event A in an experiment is 1/3. If the experiment is performed 2 times and event A did not occur, then on the third trial event A

An experiment consists of tossing 4 coins successively. The number of sample points in this experiment is

If a penny is tossed three times and comes up heads all three times, the probability of heads on the fourth trial is

Data and Statistics

Descriptive Statistics: Tabular and Graphical Presentations

Descriptive Statistics: Numerical Measures

Discrete Probability Distributions

Continuous Probability Distributions

Sampling and Sampling Distributions

Interval Estimation

Hypothesis Tests

Comparisons Involving Means, Experimental Design and Analysis of Variance

Comparisons Involving Proportions and a Test of Independence

Simple Linear Regression

Multiple Regression

Filters

If P(A) = 0.45, P(B) = 0.55, and P(A $\cup$ B) = 0.78, then P(A | B) =

If A and B are independent events with P(A) = 0.35 and P(B) = 0.20, then, P(A $\cup$ B) =

If A and B are mutually exclusive events with P(A) = 0.3 and P(B) = 0.5, then P(A $\cup$ B) =