Exam 8: Interval Estimation

A random sample of 49 lunch customers was taken at a restaurant. The average amount of time the customers in the sample stayed in the restaurant was 45 minutes with a standard deviation of 14 minutes. a.Compute the standard error of the mean. b.With a .95 probability, what statement can be made about the size of the margin of error? c.Construct a 95% confidence interval for the true average amount of time customers spent in the restaurant. d.With a .95 probability, how large of a sample would have to be taken to provide a margin of error of 2.5 minutes or less?

In a random sample of 144 observations, 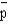= 0.6. The 95% confidence interval for P is

If the standard deviation of the lifetime of a vacuum cleaner is estimated to be 300 hours, how large of a sample must be taken in order to be 97% confident that the margin of error will not exceed 40 hours?

When constructing a confidence interval for the population mean and the standard deviation of the sample is used, the degrees of freedom for the t distribution equals

The t value for a 95% confidence interval estimation with 24 degrees of freedom is

In order to determine how many hours per week freshmen college students watch television, a random sample of 256 students was selected. It was determined that the students in the sample spent an average of 14 hours with a standard deviation of 3.2 hours watching TV per week. a.Provide a 95% confidence interval estimate for the average number of hours that all college freshmen spend watching TV per week. b.Assume that a sample of 62 students was selected (with the same mean and the standard deviation). Provide a 95% confidence interval estimate for the average number of hours that all college freshmen spend watching TV per week.

Exhibit 8-2 A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph. -Refer to Exhibit 8-2. The standard error of the mean is

The makers of a soft drink want to identify the average age of its consumers. A sample of 55 consumers was taken. The average age in the sample was 21 years with a standard deviation of 4 years. a.Construct a 95% confidence interval for the true average age of the consumers. b.Construct an 80% confidence interval for the true average age of the consumers. c.Discuss why the 95% and 80% confidence intervals are different.

A random sample of 81 credit sales in a department store showed an average sale of $68.00. From past data, it is known that the standard deviation of the population is $27.00. a.Determine the standard error of the mean. b.With a 0.95 probability, what can be said about the size of the margin of error? c.What is the 95% confidence interval of the population mean?

In developing an interval estimate, if the population standard deviation is unknown

In a random sample of 400 residents of Chattanooga, 320 residents indicated that they voted for the Democratic candidate in the last presidential election. Develop a 95% confidence interval estimate for the proportion of all Chattanooga residents who voted for the Democratic candidate.

It is known that the population variance equals 484. With a 0.95 probability, the sample size that needs to be taken if the desired margin of error is 5 or less is

Exhibit 8-2 A random sample of 121 automobiles traveling on an interstate showed an average speed of 65 mph. From past information, it is known that the standard deviation of the population is 22 mph. -Refer to Exhibit 8-2. If the sample size was 100 (other factors remain unchanged), the interval for $\mu$ would

The value added and subtracted from a point estimate in order to develop an interval estimate of the population parameter is known as the

From a population that is normally distributed, a sample of 25 elements is selected and the standard deviation of the sample is computed. For the interval estimation of $\mu$ , the proper distribution to use is the

After computing a confidence interval, the user believes the results are meaningless because the width of the interval is too large. Which one of the following is the best recommendation?

A sample of 20 items from a population with an unknown $\sigma$ is selected in order to develop an interval estimate of $\mu$ . Which of the following is not necessary?

The average score of a sample of 87 senior business majors at UTC who took the Graduate Management Admission Test was 510 with a standard deviation of 36. Provide a 98% confidence interval for the mean of the population.

In order to determine an interval for the mean of a population with unknown standard deviation a sample of 61 items is selected. The mean of the sample is determined to be 23. The number of degrees of freedom for reading the t value is

The manager of a grocery store wants to determine what proportion of people who enter his store are his regular customers. What size sample should he take so that at 97% confidence the margin of error will not be more than 0.1?