Exam 4: Extension E: Applications of Differentiation
Exam 1: Extension A: Functions and Models20 Questions
Exam 1: Extension B: Functions and Models5 Questions
Exam 1: Extension C: Functions and Models8 Questions
Exam 1: Extension D: Functions and Models12 Questions
Exam 1: Extension E: Functions and Models7 Questions
Exam 1: Extension F: Functions and Models5 Questions
Exam 2: Extension A: Limits and Derivatives9 Questions
Exam 2: Extension B: Limits and Derivatives5 Questions
Exam 2: Extension C: Limits and Derivatives6 Questions
Exam 2: Extension D: Limits and Derivatives6 Questions
Exam 2: Extension E : Limits and Derivatives5 Questions
Exam 2: Extension F: Limits and Derivatives5 Questions
Exam 2: Extension G: Limits and Derivatives10 Questions
Exam 2: Extension H: Limits and Derivatives5 Questions
Exam 3: Extension A: Differentiation Rules5 Questions
Exam 3: Extension B: Differentiation Rules11 Questions
Exam 3: Extension C: Differentiation Rules8 Questions
Exam 3: Extension D: Differentiation Rules5 Questions
Exam 3: Extension E: Differentiation Rules4 Questions
Exam 3: Extension F: Differentiation Rules5 Questions
Exam 3: Extension G: Differentiation Rules5 Questions
Exam 4: Extension A: Applications of Differentiation17 Questions
Exam 4: Extension B: Applications of Differentiation8 Questions
Exam 4: Extension C: Applications of Differentiation15 Questions
Exam 4: Extension D: Applications of Differentiation5 Questions
Exam 4: Extension E: Applications of Differentiation12 Questions
Exam 4: Extension F: Applications of Differentiation5 Questions
Exam 4: Extension G: Applications of Differentiation12 Questions
Exam 5: Extension A: Integrals5 Questions
Exam 5: Extension B: Integrals10 Questions
Exam 5: Extension C: Integrals7 Questions
Exam 5: Extension D: Integrals5 Questions
Exam 5: Extension E: Integrals7 Questions
Exam 6: Extension A: Applications of Integration9 Questions
Exam 6: Extension B: Applications of Integration14 Questions
Exam 6: Extension C: Applications of Integration7 Questions
Exam 6: Extension D: Applications of Integration5 Questions
Exam 6: Extension E: Applications of Integration5 Questions
Exam 6: Extension F: Applications of Integration6 Questions
Exam 7: Extension A: Differential Equations11 Questions
Exam 7: Extension B: Differential Equations13 Questions
Exam 7: Extension C: Differential Equations5 Questions
Exam 7: Extension D: Differential Equations8 Questions
Exam 7: Extension E: Differential Equations7 Questions
Exam 7: Extension F: Differential Equations16 Questions
Exam 7: Extension G: Differential Equations10 Questions
Exam 8: Extension A: Infinte Sequences and Series6 Questions
Exam 8: Extension B: Infinte Sequences and Series11 Questions
Exam 8: Extension C: Infinte Sequences and Series7 Questions
Exam 8: Extension D: Infinte Sequences and Series5 Questions
Exam 8: Extension E: Infinte Sequences and Series6 Questions
Exam 8: Extension F: Infinte Sequences and Series5 Questions
Exam 8: Extension G: Infinte Sequences and Series8 Questions
Exam 8: Extension H: Infinte Sequences and Series5 Questions
Exam 9: Extension A: Vectors and the Geometry of Space5 Questions
Exam 9: Extension B: Vectors and the Geometry of Space5 Questions
Exam 9: Extension C: Vectors and the Geometry of Space5 Questions
Exam 9: Extension D: Vectors and the Geometry of Space6 Questions
Exam 9: Extension E: Vectors and the Geometry of Space9 Questions
Exam 10: Extension A: Vector Functions9 Questions
Exam 10: Extension B: Vector Functions5 Questions
Exam 10: Extension C: Vector Functions5 Questions
Exam 10: Extension D: Vector Functions7 Questions
Exam 10: Extension E: Vector Functions10 Questions
Exam 10: Extension F: Vector Functions4 Questions
Exam 10: Extension H: Vector Functions5 Questions
Exam 10: Extension G: Vector Functions9 Questions
Exam 10: Extension H: Vector Functions14 Questions
Exam 11: Extension A: Partial Derivatives5 Questions
Exam 11: Extension B: Partial Derivatives13 Questions
Exam 11: Extension C: Partial Derivatives17 Questions
Exam 11: Extension D: Partial Derivatives8 Questions
Exam 11: Extension E: Partial Derivatives5 Questions
Exam 11: Extension F: Partial Derivatives5 Questions
Exam 11: Extension G: Partial Derivatives14 Questions
Exam 11: Extension H: Partial Derivatives6 Questions
Exam 12: Extension A: Multiple Integrals5 Questions
Exam 12: Extension B: Multiple Integrals10 Questions
Exam 12: Extension C: Multiple Integrals11 Questions
Exam 12: Extension D: Multiple Integrals5 Questions
Exam 12: Extension E: Multiple Integrals11 Questions
Exam 12: Extension F: Multiple Integrals5 Questions
Exam 12: Extension G: Multiple Integrals6 Questions
Exam 12: Extension H: Multiple Integrals6 Questions
Exam 13: Extension A: Vector Calculus5 Questions
Exam 13: Extension B: Vector Calculus7 Questions
Exam 13: Extension C: Vector Calculus5 Questions
Exam 13: Extension D: Vector Calculus6 Questions
Exam 13: Extension E: Vector Calculus10 Questions
Exam 13: Extension F: Vector Calculus5 Questions
Exam 13: Extension G: Vector Calculus5 Questions
Exam 13: Extension H: Vector Calculus9 Questions
Exam 13: Extension I: Vector Calculus3 Questions
Select questions type
A piece of wire 10 m long is cut into two pieces.One piece is bent into a square and the other is bent into an equilateral triangle.How should the wire be cut for the square so that the total area enclosed is a minimum? Round your answer to the nearest hundredth.
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
A
Find an equation of the line through the point (8,16) that cuts off the least area from the first quadrant.
Free
(Essay)
4.9/5  (36)
(36)
Correct Answer:
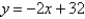
Find the dimensions of the rectangle of largest area that can be inscribed in an equilateral triangle of side L = 9 cm if one side of the rectangle lies on the base of the triangle. Round your answer to the nearest tenth.
Free
(Multiple Choice)
4.8/5  (36)
(36)
Correct Answer:
D
A woman at a point A on the shore of a circular lake with radius 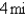 wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time.She can walk at the rate of
wants to arrive at the point C diametrically opposite on the other side of the lake in the shortest possible time.She can walk at the rate of 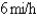 and row a boat at
and row a boat at 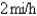 How should she proceed? (Find
How should she proceed? (Find 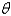 ).Round the result,if necessary,to the nearest hundredth.
).Round the result,if necessary,to the nearest hundredth. 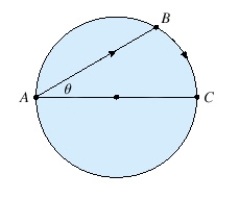
(Multiple Choice)
4.8/5  (42)
(42)
The sum of two positive numbers is 16. What is the smallest possible value of the sum of their squares?
(Short Answer)
4.9/5  (39)
(39)
Find the maximum area of a rectangle that can be circumscribed about a given rectangle with length L = 8 and width W = 3. 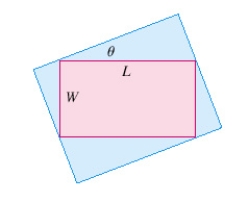
(Short Answer)
4.9/5  (38)
(38)
A farmer with 710 ft of fencing wants to enclose a rectangular area and then divide it into four pens with fencing parallel to one side of the rectangle.What is the largest possible total area of the four pens?
(Short Answer)
4.8/5  (36)
(36)
A steel pipe is being carried down a hallway 14 ft wide.At the end of the hall there is a right-angled turn into a narrower hallway 6 ft wide.What is the length of the longest pipe that can be carried horizontally around the corner? 
(Short Answer)
4.7/5  (29)
(29)
Find two positive numbers whose product is 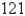 and whose sum is a minimum.
and whose sum is a minimum.
(Multiple Choice)
4.7/5  (42)
(42)
A rectangular storage container with an open top is to have a volume of 10 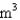 The length of its base is twice the width.Material for the base costs $12 per square meter.Material for the sides costs $5 per square meter.Find the cost of materials for the cheapest such container.
The length of its base is twice the width.Material for the base costs $12 per square meter.Material for the sides costs $5 per square meter.Find the cost of materials for the cheapest such container.
(Multiple Choice)
4.8/5  (41)
(41)
What is the minimum vertical distance between the parabolas 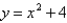 and
and 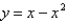 ?
?
(Short Answer)
4.8/5  (24)
(24)
Filters
- Essay(0)
- Multiple Choice(0)
- Short Answer(0)
- True False(0)
- Matching(0)